
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a=\lim\limits_{x\rightarrow3}\frac{\left(x-3\right)\left(2x+3\right)}{\left(x-3\right)\left(x^3+3x^2+9x\right)}=\lim\limits_{x\rightarrow3}\frac{2x+3}{x^3+3x^2+9x}=\frac{2.3+3}{3^3+2.3^2+9.3}=...\)
\(b=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^4+x^2+2x^3+2x+2\right)}=\frac{1+1}{1+1+2+2+2}=...\)
\(c=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)^2\left(4x^3+3x^2+2x+1\right)}{\left(x-1\right)^2\left(x^2+x+2\right)}=\frac{4+3+2+1}{1+1+2}=...\)
\(d=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{1+1+1+1+1}{1+1+1}=...\)
\(Lim_{x\rightarrow3}\frac{x^4-27x}{2x^2-3x-9}=Lim_{x\rightarrow3}\frac{x\left(x^3-3^3\right)}{\left(x-3\right)\left(2x+3\right)}\)
\(=Lim_{x\rightarrow3}\frac{x\left(x-3\right)\left(x^2+3x+9\right)}{\left(x-3\right)\left(2x+3\right)}=Lim_{x\rightarrow3}\frac{x\left(x^2+3x+9\right)}{2x+3}\)
\(=\frac{3\left(3^2+3.3+9\right)}{3.2+3}=\frac{3\left(9+9+9\right)}{9}=9\)
Vậy \(Lim_{x\rightarrow3}\frac{x^4-27x}{2x^2-3x-9}=9\)

Bài 1:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2\left|x\right|+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2x+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2+\frac{1}{x}}{3-\frac{1}{x}}=-\frac{2}{3}\)
\(b=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{9+\frac{1}{x}+\frac{1}{x^2}}-\sqrt{4+\frac{2}{x}+\frac{1}{x^2}}}{1+\frac{1}{x}}=\frac{\sqrt{9}-\sqrt{4}}{1}=1\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{1+\frac{2}{x}+\frac{3}{x^2}}+4+\frac{1}{x}}{\sqrt{4+\frac{1}{x^2}}+\frac{2}{x}-1}=\frac{1+4}{\sqrt{4}-1}=5\)
\(d=\lim\limits_{x\rightarrow+\infty}\frac{\frac{3}{x}-\frac{2}{x\sqrt{x}}+\sqrt{1-\frac{5}{x^3}}}{2+\frac{4}{x}-\frac{5}{x^2}}=\frac{1}{2}\)
Bài 2:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{1}{x}}{1-\frac{1}{x}}=2\)
\(b=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{3}{x^3}}{1-\frac{2}{x}+\frac{1}{x^3}}=2\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{x^2\left(3+\frac{1}{x^2}\right)x\left(5+\frac{3}{x}\right)}{x^3\left(2-\frac{1}{x^3}\right)x\left(1+\frac{4}{x}\right)}=\frac{15}{+\infty}=0\)

a.
\(\lim\limits_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}=\lim_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{(x-1)^3(3x+1)}=\lim\limits _{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x+1}.\lim\limits_{x\to 1+}\frac{1}{(x-1)^3}\)
\(=\frac{1}{4}.(+\infty)=+\infty \)
Hoàn toàn tương tự:
\(\lim\limits_{x\to 1-}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}=-\infty \)
Do đó: \(\lim\limits_{x\to 1+}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\neq \lim\limits_{x\to 1-}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\) nên không tồn tại \(\lim\limits_{x\to 1}\frac{2x^4-5x^3+3x^2+1}{3x^4-8x^3+6x^2-1}\)
b.
\(\lim\limits_{x\to 1+}\frac{x^3-3x^2+2}{x^4-4x+3}=\lim\limits_{x\to 1+}\frac{(x-1)(x^2-2x-2)}{(x-1)^2(x^2+2x+3)}=\lim\limits_{x\to 1+}\frac{x^2-2x-2}{(x-1)(x^2+2x+3)}\)
\(=\lim\limits_{x\to 1+}\frac{x^2-2x-2}{x^2+2x+3}.\lim\limits_{x\to 1+}\frac{1}{x-1}=\frac{-1}{2}.(+\infty)=-\infty \)
Tương tự \(\lim\limits_{x\to 1-}\frac{x^3-3x^2+2}{x^4-4x+3}=+\infty \)
Do đó không tồn tại \(\lim\limits_{x\to 1}\frac{x^3-3x^2+2}{x^4-4x+3}\)
c.
\(\lim\limits_{x\to 1}\frac{x^3-2x-1}{x^5-2x-1}=\frac{1^3-2.1-1}{1^5-2.1-1}=1\)
d.
\(\lim\limits_{x\to -1}\frac{(x+2)^2-1}{x^2-1}=\lim\limits_{x\to -1}\frac{(x+2-1)(x+2+1)}{(x-1)(x+1)}=\lim\limits_{x\to -1}\frac{x+3}{x-1}=-1\)

\(a=\lim\limits_{x\rightarrow0}\frac{x^2}{x\left(\sqrt{1+x^2}+1\right)}=\lim\limits_{x\rightarrow0}\frac{x}{\sqrt{1+x^2}+1}=\frac{0}{2}=0\)
\(b=\lim\limits_{x\rightarrow1}\frac{\sqrt[3]{x+7}-2+2-\sqrt{5-x^2}}{x-1}=\lim\limits_{x\rightarrow1}\frac{\frac{x-1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}+\frac{\left(x-1\right)\left(x+1\right)}{2+\sqrt{5-x^2}}}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\frac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}+\frac{x+1}{2+\sqrt{5-x^2}}\right)=\frac{1}{12}+\frac{1}{2}=\frac{7}{12}\)
\(c=\lim\limits_{x\rightarrow0}\frac{2x}{x\left(\sqrt[3]{\left(1+x\right)^2}+\sqrt[3]{\left(1+x\right)\left(1-x\right)}+\sqrt[3]{\left(1-x\right)^2}\right)}=\lim\limits_{x\rightarrow0}\frac{2}{\sqrt[3]{\left(1+x\right)^2}+\sqrt[3]{\left(1+x\right)\left(1-x\right)}+\sqrt[3]{\left(1-x\right)^2}}=\frac{2}{3}\)
\(d=\frac{\sqrt[3]{6}}{0}=+\infty\)

a)  (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) =  x4(1 -
x4(1 - 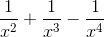 ) = +∞.
) = +∞.
b)  (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) =  x3(-2 +
x3(-2 + 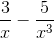 ) = +∞.
) = +∞.
c) 
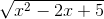 =
= 
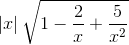 = +∞.
= +∞.
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left|x\right|\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{x\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}+1}{\dfrac{5}{x}-2}=-1\).

Bài 1:
\(a=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\lim\limits_{x\rightarrow-1}\frac{x^4-x^3+x^2-x+1}{x^2-x+1}=\frac{5}{3}\)
\(b=\frac{1-5+1}{0}=\frac{-3}{0}=-\infty\)
\(c=\lim\limits_{x\rightarrow1}\frac{x\left(1+2x\right)\left(1+3x\right)+2x\left(1+3x\right)+3x}{x}=\lim\limits_{x\rightarrow1}\left[\left(1+2x\right)\left(1+3x\right)+2\left(1+3x\right)+3\right]=1+2+3=6\)
\(d=\lim\limits_{x\rightarrow0}\frac{5\left(1+x\right)^4-1}{5x^4+2x}=\frac{4}{0}=+\infty\)
Bài 2:
\(a=\lim\limits_{x\rightarrow1}\frac{x^m-1}{x^n-1}=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)
\(b=\lim\limits_{x\rightarrow a}\frac{x-a}{x^n-a^n}=\lim\limits_{x\rightarrow a}\frac{1}{nx^{n-1}}=\frac{1}{n.a^{n-1}}\)
\(c=\lim\limits_{x\rightarrow0}\frac{x+x^2+...+x^n-n}{x-1}=\frac{-n}{-1}=n\)
\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)=x\left(1+2x\right)...\left(1+nx\right)+\left(1+2x\right)\left(1+3x\right)...\left(1+nx\right)\)
\(=x\left(1+2x\right)...\left(1+nx\right)+2x\left(1+3x\right)...\left(1+nx\right)+\left(1+3x\right)...\left(1+nx\right)\)
\(=...\)
\(=x\left(1+2x\right)...\left(1+nx\right)+2x\left(1+3x\right)...\left(1+nx\right)+...+nx+1\)
\(\Rightarrow\lim\limits_{x\rightarrow0}\frac{\left(1+2x\right)\left(1+3x\right)...\left(1+nx\right)-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\frac{x\left(1+2x\right)...\left(1+nx\right)+2x\left(1+3x\right)...\left(1+nx\right)+...+nx}{x}\)
\(=\lim\limits_{x\rightarrow0}\left[\left(1+2x\right)...\left(1+nx\right)+2\left(1+3x\right)...\left(1+nx\right)+...+n\right]\)
\(=1+2+3+...+n=\frac{n\left(n+1\right)}{2}\)

\(a=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x^2+x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x+1\right)\left(x^2+1\right)}{x^2+x-1}=\frac{4}{1}=4\)
\(b=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\lim\limits_{x\rightarrow-1}\frac{x^4-x^3+x^2-x+1}{x^2-x+1}=\frac{5}{3}\)
\(c=\lim\limits_{x\rightarrow3}\frac{\left(x+1\right)\left(x-3\right)^2}{\left(x^2+1\right)\left(x^2-9\right)}=\lim\limits_{x\rightarrow3}\frac{\left(x+1\right)\left(x-3\right)}{\left(x^2+1\right)\left(x+3\right)}=\frac{0}{60}=0\)
\(d=\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+x}{x^2-2x+1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4+1}{2x-2}=\lim\limits_{x\rightarrow1}\frac{120x^4-100x^3}{2}=10\)
\(e=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)
\(f=\lim\limits_{x\rightarrow-2}\frac{\left(x+2\right)\left(x-2\right)\left(x^2+4\right)}{\left(x+2\right)x^2}=\lim\limits_{x\rightarrow-2}\frac{\left(x-2\right)\left(x^2+4\right)}{x^2}=-8\)
Hai câu d, e khai triển thì dài quá nên làm biếng sử dụng L'Hopital
Ta có:
Chọn A.