Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài của mảnh đất hcn là x(m),chiều rộng của mảnh đất hcn là y(m) (0<y<x).
Diện tích ban đầu của mảnh đất đó là : xy(m2).
Sau khi tăng chiều dài 2m và chiều rộng thêm 5m thì diện tích mới của mản đất đó là:(x+2)(y=5) (m2). (1)
Vì nếu tăng chiều dài 2m và chiều rộng thêm 5m thì diện tích tăng thêm 120m2,nên ta có pt:(x+2)(y=5) -xy=120.
Sau khi giảm chiều dài 3m và chiều rộng đi 2m thì diện tích của mảnh đất đó là: (x-3)(y-2) (m2).
Vì Nếu giảm chiều dài 3m và chiều rộng đi 2m thì diện tích giảm 60m2,nên ta có pt : xy-(x-3)(y-2)=60. (2)
- Còn lại hệ pt tự giải nốt nhé

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng
240
m
2
⇒
Δ
=
3
2
–
4
.
1
.
(
-
180
)
=
729
⇒ Chiều dài mảnh đất là: 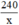 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
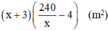
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
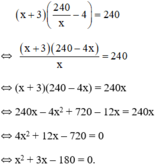
Có a = 1; b = 3; c = -180
Phương trình có hai nghiệm:
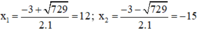
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng 240 m2 ⇒ Chiều dài mảnh đất là: 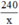 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
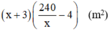
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
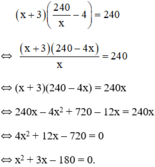
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
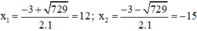
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều dài của mảnh đất hình chữ nhật là x (m, x > 4)
Khi đó chiều rộng của mảnh đất hình chữ nhật là \(\frac{240}{x}\left(m\right)\)
Khi tăng chiều rộng 3m, giảm chiều dài 4m thì diện tích mảnh đất là:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)\)
Do diện tích không đổi nên ta có phương trình:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow240+3x-\frac{960}{x}-12=240\)
\(\Rightarrow3x^2-12x-960=0\Rightarrow\orbr{\begin{cases}x=20\left(n\right)\\x=-16\left(l\right)\end{cases}}\)
Vậy chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 12m.

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: ab=280 và (a+10)(b-3)=ab+220
=>-3a+10b=250 và ab=280
=>-3a=250-10b và ab=280
=>a=10/3b-250/3 và b(10/3b-250/3)=280
=>b=28
=>a=10

Bài giải:
Gọi chiều rộng của mảnh đất là x (m), x > 0.
Vì diện tích của mảnh đất bằng 240 m2 nên chiều dài là: (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là x + 3 (m), chiều dài là (240/X - 4) (m) và diện tích là:
(x + 3)( 240/x- 4) ( m2 )
Theo đầu bài ta có phương trình: (x + 3)(240/x - 4) = 240
Giải phương trình:
Từ phương trình này suy ra:
-4x2 – 12x + 240x + 720 = 240x hay:
x2 + 3x – 180 = 0
Giải phương trình: ∆ = 32 + 720 = 729, √∆ = 27
x1 = 12, x2 = -15
Vì x > 0 nên x2 = -15 không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là 12m, chiều dài là: 240 : 12 = 20(m)
Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m.
Bài giải:
Gọi chiều rộng của mảnh đất là x (m), x > 0.
Vì diện tích của mảnh đất bằng 240 m2 nên chiều dài là: (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là x + 3 (m), chiều dài là ( - 4) (m) và diện tích là:
(x + 3)( - 4) ( m2 )
Theo đầu bài ta có phương trình: (x + 3)( - 4) = 240
Giải phương trình:
Từ phương trình này suy ra:
-4x2 – 12x + 240x + 720 = 240x hay:
x2 + 3x – 180 = 0
Giải phương trình: ∆ = 32 + 720 = 729, √∆ = 27
x1 = 12, x2 = -15
Vì x > 0 nên x2 = -15 không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là 12m, chiều dài là: 240 : 12 = 20 (m)
Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m.

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có:
a*b=600 và (a-2)(b-2)=ab-96
=>-2(a+b)+4=-96 và a*b=600
=>-2(a+b)=-100 và a*b=600
=>a+b=50 và a*b=600
=>a=30; b=20

Gọi 2 kích thước của hình chữ nhật là x và y(ĐK:x,y>0)
Diện tích của hình chữ nhật là xy
Nếu tăng chiều rộng thêm 3m và chiều dài giảm đi 4 m thì diện tích của hình chữ nhật là (x+3).(y-4).
Theo bài ra ta có hệ phương trình:
xy=240
{ ⇔x=12;y=20 Vậy chiều rộng HCN là 12,chiều dài HCN là 20
(x+3).(y-4)=xy
Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.

Gọi chiều dài mảnh đất là x(m), chiều rộng mảnh đất là y(m)
(Điều kiện: x>0; y>0;x>y)
Diện tích mảnh đất là 60m2 nên xy=60
Nếu giảm bớt mỗi cạnh đi 2m thì diện tích còn lại là 32m2 nên ta có:
(x-2)(y-2)=32
=>xy-2x-2y+4=32
=>60-2x-2y+4=32
=>64-2(x+y)=32
=>2(x+y)=32
=>x+y=16
mà xy=60
nên x,y là các nghiệm của phương trình:
\(a^2-16a+60=0\)
=>(a-6)(a-10)=0
=>\(\left[{}\begin{matrix}a=6\\a=10\end{matrix}\right.\)
mà x>y
nên x=10;y=6
vậy: Chiều dài là 10m; chiều rộng là 6m