Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

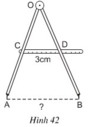
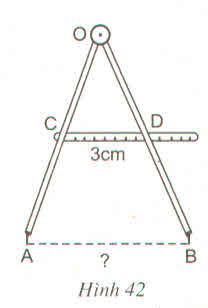
Ta có: CO = CA (gt)
DO = DB (gt)
⇒ CD là đường trung bình của ΔOAB
⇒ AB = 2CD = 2.3 = 6cm.

Bài giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
Ta có: CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ΔOAB
Suy ra AB = 2CD = 2.3 = 6cm

a)
Vẽ hình đúng đến câu a

Lập luận được điểm A nằm giữa hai điểm O và B
Tính được AB = 6cm
b)Lập luận chứng tỏ được A là trung điểm của đoạn thẳng OB
Lập luận tính được OM = 3cm
c)Lập luận chứng tỏ điểm M nằm giữa hai điểm O và B
Suy ra OM + MB = OB
Tính MB = 9cm
d)Lập luận chứng tỏ được điểm O nằm giữa hai điểm M và N
Chỉ ra được OM = ON và kết luận ) là trung điểm của đoạn thẳng MN
Vì OA=6,OB=12 nên AB=12-6=6
Vì OA<OB(6<12) suy ra A nằm giữa O và B 1
Mà OA=6,AB=6 2
Từ 1 và 2 suy ra A là trung điểm của đoạn thẳng OB
Vì M là trung điểm của OA nên OM=OA/2=3
Ta có OM=3,OB=12 nên MB=12-3=9
Vì ON thuộc tia đối của tia Ox nên O nằm giữa N và M 3
Lại có OM=ON=3 4
Từ 3 va 4 suy ra O là trung điểm của MN

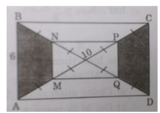
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ
⇒ Tứ giác MNPQ là hình bình hành.
Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.
Trong ΔABC ta có

Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).
b)Dễ thấy ΔAOB = ΔCOD (c.c.c).
Tương tự ΔMON = ΔPOQ
Do đó: SAOB = SCOD và SMON = SPOQ.
⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.

a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
a) Xét ΔDOC và ΔBOA có
\(\widehat{DOC}=\widehat{BOA}\)(hai góc đối đỉnh)
\(\widehat{DCO}=\widehat{BAO}\)(hai góc so le trong, DC//AB)
Do đó: ΔDOC\(\sim\)ΔBOA(g-g)
Suy ra: \(\dfrac{OD}{OB}=\dfrac{OC}{OA}=\dfrac{DC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{1}{3}=\dfrac{OC}{12}=\dfrac{CD}{18}\)
\(\Leftrightarrow\left\{{}\begin{matrix}OC=\dfrac{12}{3}=4\left(cm\right)\\CD=\dfrac{18}{3}=6\left(cm\right)\end{matrix}\right.\)
Vậy: OC=4cm; CD=6cm

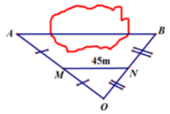
Xét tam giác OAB ta có:
C là trung điểm của OA (1)
D là trung điểm của OB (2)
Từ (1)(2) => CD là đường trung bình của tam giác OAB
=> CD=1/2AB
=>AB = CD x 2 =5 x 2 =10 (cm )
P/s tham khảo nha

a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
b: Vì A nằm giữa O và B
nên OA+AB=OB
hay AB=3(cm)
c: Ta có: A nằm giữa O vàB
mà AO=AB
nên A là trung điểm của OB
d: IK=OB/2=3cm


Nên CD là đường trung bình của ∆OAB.
Do đó CD =\(\frac{1}{2}\) AB
Suy ra AB = 2CD = 2.3 = 6cm.