
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(x-3\right)\left(x-4\right)=\left(x-5\right)^2\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)-\left(x-5\right)^2=0\)
\(\Leftrightarrow x^2-4x-3x+12-\left(x^2-10x+25\right)=0\)
\(\Leftrightarrow x^2-4x-3x+12-x^2+10x-25=0\)
\(\Rightarrow3x-13=0\)
\(\Rightarrow3x=13\)
\(\Rightarrow x=\frac{13}{3}\)

(x+2)(x+4)(x+6)(x+8)+16
=(x+2)(x+8)(x+4)(x+6)+16
=(x2+10x+16)(x2+10x+24)+16
đặt t=x2+10x+16 ta được:
t.(t+8)+16
=t2+8t+16
=(t+4)2
thay t=x2+10x+16 ta được:
(x2+10x+16)2
=[(x+2)(x+8)]2
=(x+2)2(x+8)2
vậy (x+2)(x+4)(x+6)(x+8)+16 =(x+2)2(x+8)2
(x+2)(x+4)(x+6)(x+8)+16
=(x+2)(x+8)(x+4)(x+6)+16
=(x2+10x+16)(x2+10x+24)+16
đặt t=x2+10x+16 ta được:
t.(t+8)+16
=t2+8t+16
=(t+4)2
thay t=x2+10x+16 ta được:
(x2+10x+16)2
=[(x+2)(x+8)]2
=(x+2)2(x+8)2
vậy (x+2)(x+4)(x+6)(x+8)+16 =(x+2)2(x+8)2

Đây nè bạn. Mk chỉ mới nghĩ ra cách này thôi à!!! Bạn nào có cách nào thì bảo mk với nhé!!!
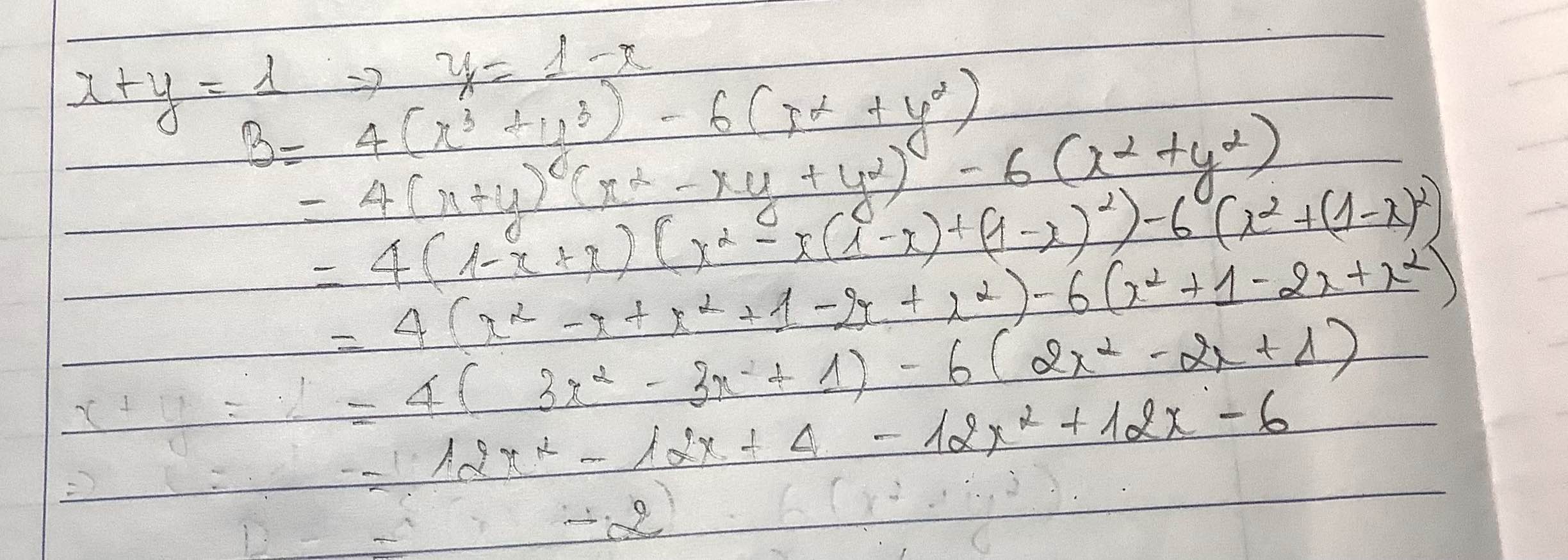
\(B=4\left(x+y\right)\left(x^2+y^2-xy\right)-6\left[\left(x+y\right)^2-2xy\right]\)
\(=4\left[\left(x+y\right)^2-3xy\right]-6\left(1-2xy\right)\)
\(=4-12xy-6+12xy\)
\(=-2\)

`(3x+2)/3 <= (x-4)/7`
`<=>7(3x+2) <= 3(x-4)`
`<=> 21x+14<=3x-12`
`<=>18x <= -26`
`<=> x <=-13/9`

\(\frac{16}{\sqrt{x-6}}+\frac{4}{\sqrt{y-2}}+\frac{256}{\sqrt{z-1750}}+\sqrt{x-6}+\sqrt{y-2}+\sqrt{z-1750}=44\) (Điều kiện xác định : \(x>6;y>2;z>1750\))
\(\Leftrightarrow\left(\sqrt{x-6}+\frac{16}{\sqrt{x-6}}-8\right)+\left(\sqrt{y-2}+\frac{4}{\sqrt{y-2}}-4\right)+\left(\sqrt{z-1750}+\frac{256}{\sqrt{z-1750}}-32\right)=0\)
\(\Leftrightarrow\frac{\left(x-6\right)-8\sqrt{x-6}+16}{\sqrt{x-6}}+\frac{\left(y-2\right)-4\sqrt{y-2}+4}{\sqrt{y-2}}+\frac{\left(z-1750\right)-32\sqrt{z-1750}+256}{\sqrt{z-1750}}=0\)
\(\Leftrightarrow\frac{\left(\sqrt{x-6}-4\right)^2}{\sqrt{x-6}}+\frac{\left(\sqrt{y-2}-2\right)^2}{\sqrt{y-2}}+\frac{\left(\sqrt{z-1750}-16\right)^2}{\sqrt{z-1750}}=0\)
Vì \(\frac{\left(\sqrt{x-6}-4\right)^2}{\sqrt{x-6}}\ge0\) , \(\frac{\left(\sqrt{y-2}-2\right)^2}{\sqrt{y-2}}\ge0\) , \(\frac{\left(\sqrt{z-1750}-16\right)^2}{\sqrt{z-1750}}\ge0\) với mọi x>6 , y>2 , z>1750 nên phương trình trên tương đương với :
\(\begin{cases}\frac{\left(\sqrt{x-6}-4\right)^2}{\sqrt{x-6}}=0\\\frac{\left(\sqrt{y-2}-2\right)^2}{\sqrt{y-2}}=0\\\frac{\left(\sqrt{z-1750}-16\right)^2}{\sqrt{z-1750}}=0\end{cases}\) \(\Leftrightarrow\begin{cases}\left(\sqrt{x-6}-4\right)^2=0\\\left(\sqrt{y-2}-2\right)^2=0\\\left(\sqrt{z-1750}-16\right)^2=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=22\\y=6\\z=2006\end{cases}\) (TMĐK)
Vậy (x;y;z) = (22;6;2006)

\(16^2\)- \(x^{2^2}\)
=>(16-\(x^2\))(16+\(x^2\))