OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

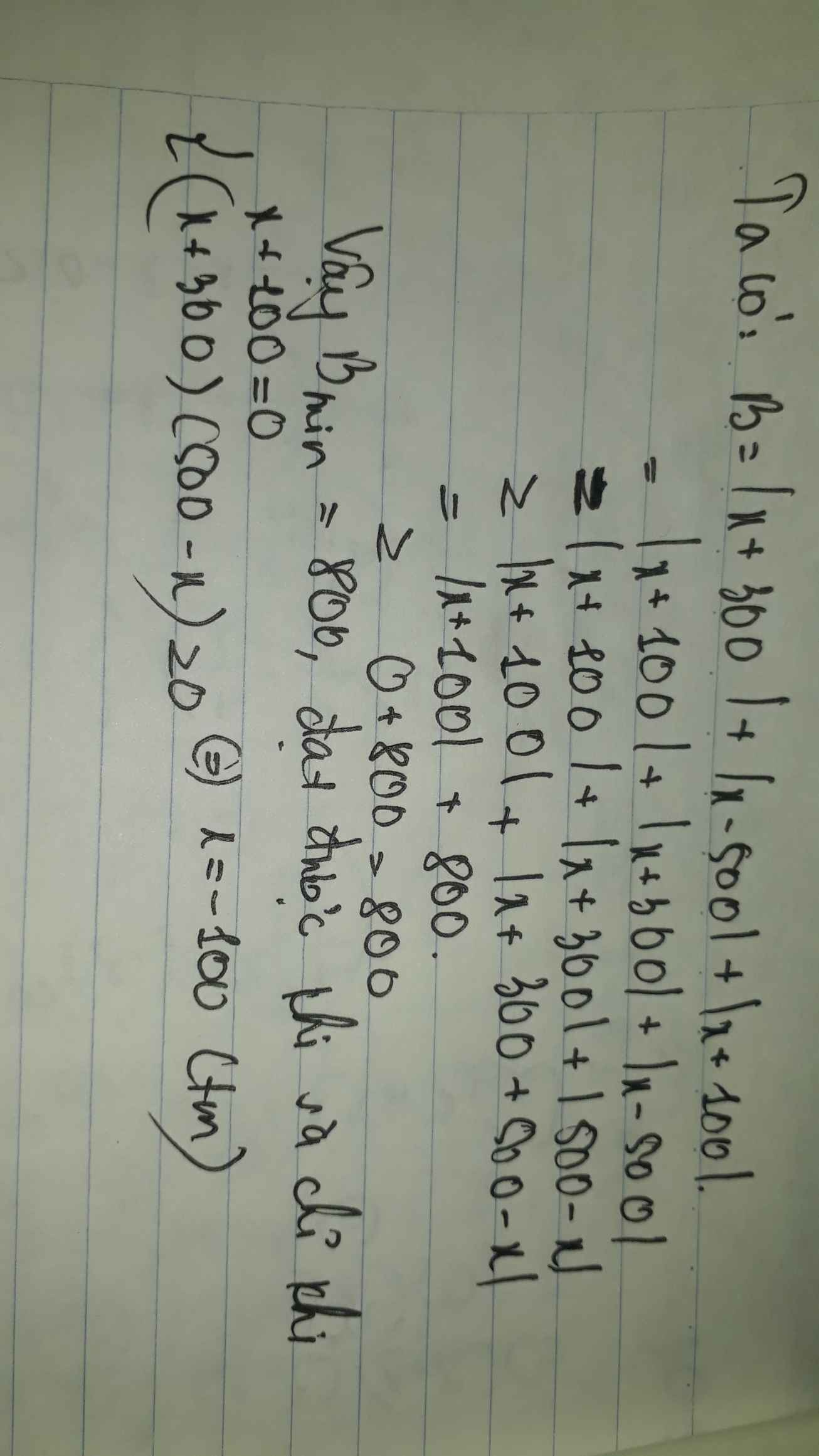
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
YS
Yoona SNSD
21 tháng 9 2016 - olm

Bài 1: Tìm x, y biết: 

\(\left|x-3,5\right|+\left|y-1,3\right|=0\)

Bài 2: Tìm GTNN của biểu thức :

A= \(\left|x-500\right|+\left|x-300\right|\)

Các bạn giải cho mk với! =*-*=
#Toán lớp 7
2
DT
dang thi hoa
21 tháng 9 2016

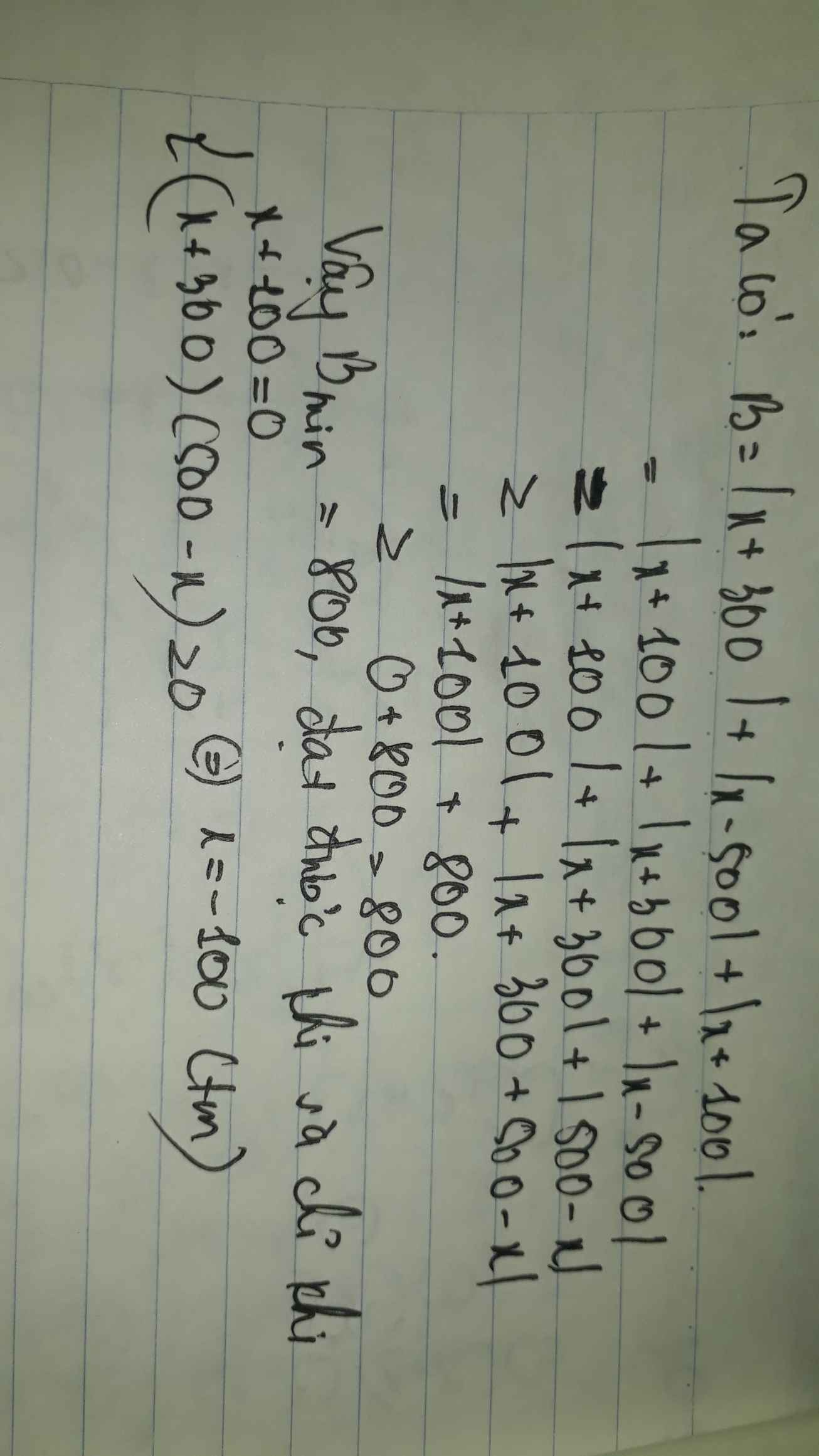
bai 1 :Ta co |x-3,5| >hoac=0

              va |y-1,3| >hoac=0 nen |x-3,5|+|y-1,3|=0 <=> x-3,5=0 va y-1,3=0

                                                                        =>x=-3,5 va y=-1,3

bai 2:   ta co

A=|x-500| +|x-300| =|x-500|+|300-x|

=>A > hoac =|x-500+300-x|=|-200|=200

dau = xay ra<=>(x-500).(300-x)=0 =>300< hoac=x< hoac =500


 

                 

Đúng(0)
CC
Công chúa Sakura
21 tháng 9 2016

Bài 1 :

Ta có : \(\left|x-3,5\right|\ge0\) với mọi x

            \(\left|y-1,3\right|\ge0\) với mọi x

 \(\Rightarrow\left|x-3,5\right|+\left|y-1,3\right|\ge0\) với mọi x

Mà \(\left|x-3,5\right|+\left|y-1,3\right|=0\)

\(\Rightarrow\hept{\begin{cases}\left|x-3,5\right|=0\\\left|y-1,3\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x-3,5=0\\y-1,3=0\end{cases}}\Rightarrow\hept{\begin{cases}x=3,5\\y=1,3\end{cases}}\)

Bài 2 :

Ta có : \(\left|x-500\right|\ge0\) với mọi x

            \(\left|x-300\right|\ge0\) với mọi x

\(\Rightarrow\left|x-500\right|+\left|x-300\right|\ge0\) với mọi x

Câu này mk ko bít, làm tới đây đc thôi à

Đúng(0)
NT
Nguyễn Tiến Dũng
3 tháng 4 2017

Tìm GTNN của C=\(\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+....+\left|x-100\right|\)
#Toán lớp 7
2
MP
Mysterious Person
21 tháng 8 2018

ta có : \(C=\left|x-1\right|+\left|2-x\right|+\left|x-3\right|+\left|4-x\right|+...+\left|x-99\right|+\left|100-x\right|\)

\(\ge\left|x-1+2-x+x-3+4-x+...+x-99+100-x\right|=\left|50\right|=50\)

\(\Rightarrow C_{min}=50\)

dấu bằng xảy ra khi : \(x-1;x-2;x-3;...;x-100>0\Leftrightarrow x>100\)

vậy GTNN của \(C\) là \(50\) khi \(x>100\)

Đúng(0)
EC
EDOGAWA CONAN
21 tháng 8 2018

50

Đúng(0)
F
FFPUBGAOVCFLOL
6 tháng 3 2020 - olm

Tìm GTNN của \(B=\left|x-1\right|+\left|x-2\right|+...+\left|x-100\right|\)
#Toán lớp 7
0
F
FFPUBGAOVCFLOL
6 tháng 3 2020 - olm

Tìm GTNN của \(B=\left|x-1\right|+\left|x-2\right|+...+\left|x-100\right|\)
#Toán lớp 7
1
KN
Kiệt Nguyễn
6 tháng 3 2020

Áp dụng BĐT \(\left|x\right|+\left|y\right|\ge\left|x+y\right|\):

\(\left|x-1\right|+\left|x-100\right|\ge\left|\left(x-1\right)+\left(100-x\right)\right|=99\)

(Dấu "=" khi \(1\le x\le100\))

\(\left|x-2\right|+\left|x-99\right|\ge\left|\left(x-2\right)+\left(99-x\right)\right|=97\)

(Dấu "=" khi \(2\le x\le99\))

\(\left|x-3\right|+\left|x-98\right|\ge\left|\left(x-3\right)+\left(98-x\right)\right|=95\)

(Dấu "=" khi \(3\le x\le98\))

...

\(\left|x-49\right|+\left|x-50\right|\ge\left|\left(x-49\right)+\left(50-x\right)\right|=1\)

(Dấu "="\(\Leftrightarrow49\le x\le50\))

Vậy \(B\ge99+97+95+...+1=\frac{\left(99+1\right)\left[\left(99-1\right):2+1\right]}{2}\)

\(=2500\)

Dấu "=" khi \(49\le x\le50\)

Đúng(0)
F
FFPUBGAOVCFLOL
6 tháng 3 2020 - olm

Tìm GTNN của \(B=\left|x-1\right|+\left|x-2\right|+...+\left|x-100\right|\)
#Toán lớp 7
0
DV
Đức Vương Hiền
7 tháng 2 2019

Tìm GTNN của các biểu thức

a, A=\(\left|x-2011\right|+\left|x-2012\right|\)

b, B = \(\left|x-2010\right|+\left|x-2011\right|+\left|x-2012\right|\)

c, C = \(\left|x-1\right|+\left|x-2\right|+....+\left|x-100\right|\)
#Toán lớp 7
0
TT
Thịnh Thái Nguyễn
1 tháng 3 2020 - olm

\(C=\left|x-500\right|+\left|x-300\right|\)
#Toán lớp 7
3
KK
KCLH Kedokatoji
1 tháng 3 2020

Câu hỏi là gì? Tìm min C à? min C=200 tại \(300\le x\le500\)

Đúng(0)
NT
Nguyễn Thái Thịnh
1 tháng 3 2020

Đề bài là tìm giá trị nhỏ nhất hả bạn!

Ta có: \(x=\frac{a}{b},y=\frac{c}{d}\left(a,b,c\in Z;b,d\ne0\right)\)

\(\left|\frac{a}{b}+\frac{c}{d}\right|=\left|\frac{ad+cd}{bd}\right|=\frac{\left|ad+cb\right|}{\left|bd\right|}\left(1\right)\)

Với \(a,b,c,d\)là những số nguyên ta luôn có:

\(\left|ad+cb\right|\le\left|ad\right|+\left|cb\right|\)

\(\Rightarrow\frac{\left|ad\right|}{\left|bd\right|}+\frac{\left|cb\right|}{\left|bd\right|}=\left|\frac{a}{b}\right|+\left|\frac{c}{d}\right|=\left|x\right|+\left|y\right|\left(2\right)\)

Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\left|x+y\right|\le\left|x\right|+\left|y\right|\)

Áp dụng tính chất trên ta có:

\(C=\left|x-500\right|+\left|x-300\right|\ge\left|x-500+x-300\right|\)

Ta có:

\(\left|x-500+x-300\right|=0\)

\(\Rightarrow x-500+x-300=0\)

\(\Rightarrow x+x-500-300=0\)

\(\Rightarrow x+x-\left(500+300\right)=0\)

\(\Rightarrow x+x-800=0\)

\(\Rightarrow x+x=800\)

\(\Leftrightarrow x=400\)

Vậy giá trị nhỏ nhất của C là 0 đạt được khi \(x=400\)

Đúng(0)
HM
Hà My Trần
28 tháng 10 2016 - olm

Bài 1 : Tìm GTNN của : \(A=\left|x+8\right|+\left|2x+7\right|+\left|3x+6\right|+\left|4x-7\right|+\left|3x-6\right|+\left|2x-7\right|+\left|x-8\right|-100\)
#Toán lớp 7
0
KH
Kamato Heiji
5 tháng 6 2020

Tìm GTNN của D = \(\left|\frac{x}{5}-\frac{y}{7}\right|+\left|2z-3x\right|+\left|xy+yz-500+zx\right|\)
#Toán lớp 7
0
KH
Kamato Heiji
5 tháng 6 2020

Em cảm ơn cj

Đúng(0)
TT
Thu Thao
5 tháng 6 2020

Hàn Thất Chị? Ko có chi~

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP