

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a , Góc đáy bằng : (180-50)/2= 65 độ
b Góc ở đỉnh bằng 180 - 2.50 = 80 độ

Lời giải:
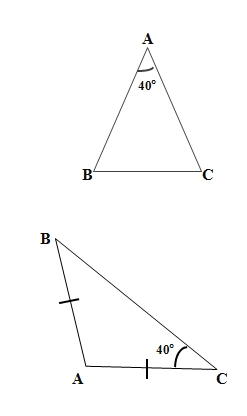
a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh A bằng 40o. Ta có:
a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh A bằng 40o. Ta có:
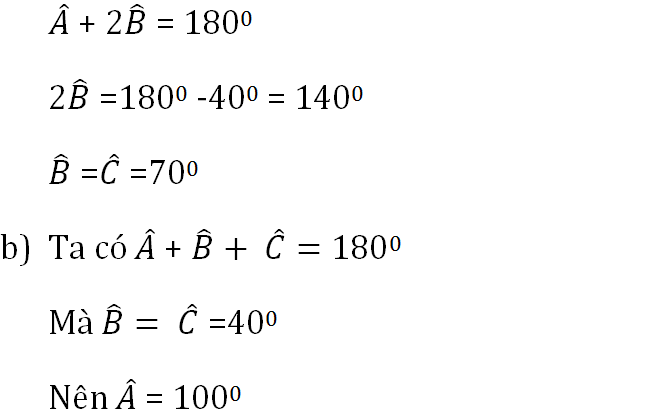

a) b) A B C B C A ABC cân tại A có C=B=50 ABC có A+B+C=180 A+50+50=180 A=80 ABC có A+B+C=180 70+2B=180 2B=180-70 2B=110 B=110:2 B=55 50 70

Gọi tam giác đó là \(\Delta\)ABC cân tại A (B=C)
a. theo đề ta có: A=400
trong tam giác ABC có:
A+B+C=1800
=> 400+B+C=1800
=> B+C=1800-400
=> B+C=1400
=> B=C=1400:2=700
b. theo đề ta có: B=C=400
trong tam giác ABC có:
A+B+C=1800
=> A+400+400=1800
=> A+800=1800
=> A=1800-800
=> A=1000

a) Nếu góc ở đỉnh cân là 1100 thì tổng 2 góc ở đáy là : 1800 - 1100 = 700 mà 2 góc ở đáy bằng nhau
=> 2 góc còn lại đều bằng : 700 : 2 = 350
Nếu góc ở đáy là 1100 thì trái với tổng 3 góc của 1 tam giác vì riêng tổng 2 góc ở đáy là : 1100 x 2 = 2200 > 1800
b) Tương tự,nếu góc ở đỉnh cân là a0 thì 2 góc còn lại ở đáy bằng nhau và đều bằng :\(\frac{180-a^0}{2}=90^0-\frac{a^0}{2}\)
Nếu góc ở đáy là a0 thì góc ở đáy kia cũng là a0 ; góc ở đỉnh cân là : 1800 - 2a0
a) tam giác đó cân ở góc 110 độ
=> 2 góc bên bằng : (180 - 110) / 2 = 35 độ
b) TH1 tam giác đó cân ở góc a độ
=> 2 góc bên bằng (180 - a ) / 2
TH2 : góc bên là a độ
=> góc bên còn lại là a độ
góc cân bằng : 180 - 2a

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 180*
B^1 + B^2 = 180*
C^1 + C^2 = 180*
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180*
mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*
Ta có: góc ngoài của một tam giác bằng tổng 2 góc trong ko kề với nó
=> Tổng 3 góc ngoài của 1 tam giác bằng tổng 2 lần các góc trong ko kề với nó
Mà tổng 2 lần các góc trong ko kề với nó = 2 x (tổng 3 góc của 1 tam giác) = 2 x 1800 = 3600
Vậy tổng ba góc ngoài ở ba đỉnh của một tam giác bằng 3600

Vì tam giác ABC cân tại đỉnh A
\(\Rightarrow\widehat{A}=\widehat{B}=\frac{\left(180-100\right)}{2}=40\)
vậu số đo mỗi góc ở đáy là 40 độ
k hộ học tốt

Bài 2:
\(\widehat{ADB}=180^0-80^0=100^0\)
Ta có: \(\widehat{ADB}+\widehat{BAD}+\widehat{B}=\widehat{ADC}+\widehat{CAD}+\widehat{C}\)
\(\Leftrightarrow\widehat{B}+100^0=\widehat{C}+80^0\)
\(\Leftrightarrow1.5\widehat{C}-\widehat{C}=-20^0\)
\(\Leftrightarrow\widehat{C}=40^0\)
hay \(\widehat{B}=60^0\)
=>\(\widehat{BAC}=80^0\)

\(\Delta ABC\)cân ở B, \(\widehat{ABC}=80^0\)nên \(\widehat{BAC}=\widehat{BCA}=50^0\)
Vì \(\widehat{IAC}=20^0,\widehat{ICA}=30^0\)nên \(\widehat{IAB}=40^0,\widehat{ICB}=20^0\)
B A C K I
Kẻ tia phân giác của \(\widehat{BAI}\)cắt tia CI ở K,ta có \(\widehat{BAK}=\widehat{KAI}=20^0\)
=> \(\widehat{KAC}=30^0=\widehat{KCA}\).Tam giác KAC cân tại ở K nên KA = KC
Xét \(\Delta AKB\)và \(\Delta CKB\)có :
AK = CK(gt)
AB = CB(gt)
KB cạnh chung
=> \(\Delta AKB=\Delta CKB\left(c-c-c\right)\)
=> \(\widehat{AKB}=\widehat{BKC}\)
Và \(\widehat{KBA}=\widehat{KBC}=40^0\)
Lại có : \(\widehat{KCB}=20^0\),vì thế \(\widehat{CKB}=120^0=\widehat{AKB}\)
Tam giác cân AKC có hai góc ở đáy bằng nhau và bằng 300 nên góc ở đỉnh \(\widehat{AKC}=120^0\)
\(\Delta AKB=\Delta AKI\left(g-c-g\right)\)nên góc ở đỉnh \(\widehat{BAI}=40^0\)
Do đó \(\widehat{AIB}=70^0\)