Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
Chọn D
Đường thẳng: 3x+ y – 8= 0 có VTPT n 1 → ( 3 ; 1 )
Đường thẳng: 4x- 2y+ 10= 0 có VTPT n 2 → ( 4 ; - 2 )
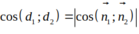
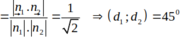

Đáp án A
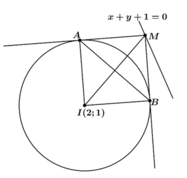
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
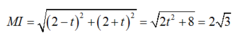
- Do đó : 2t2+ 8= 12
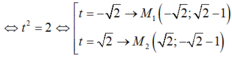

cos(d,d')=\(\dfrac{\left|1.1+2.\left(-3\right)\right|}{\sqrt{1^2+2^2}.\sqrt{1^2+\left(-3\right)^2}}\)= \(\dfrac{\sqrt{2}}{2}\)=450
Góc giữa hai đường thẳng d: x - 2y - 3 = 0 và d': 3x - y - 3 = 0 là:
A. 30 °
B. 45 °
C. 60 °
D. 90 °

Đáp án: B
d: x - 2y - 3 = 0 có 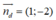
d': 3x - y - 3 = 0 có 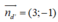
Gọi α là góc giữa hai đường thẳng d và d’
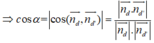
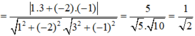
⇒ α = 45 °

NX: \(\dfrac{2}{4}\)=\(\dfrac{-1}{-2}\)≠\(\dfrac{-2}{6}\)
=> (d) // (d')
Ta lấy điểm A(0;-2) ∈ d
d(d;d') = \(\dfrac{\left|4.0-2.\left(-2\right)+6\right|}{\sqrt{4^2+2^2}}\) = \(\sqrt{5}\)
=> Chọn C

Chọn C.
Ta có:
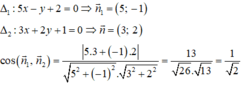
Vậy góc giữa hai đường thẳng Δ1, Δ2 là 45 ° .

Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=3\)
a. \(\overrightarrow{IM}=\left(0;2\right)\Rightarrow IM=\sqrt{0^2+2^2}=2< R\Rightarrow\) M nằm trong đường tròn
b. \(d\left(I;d\right)=\dfrac{\left|2-\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=2\sqrt{2}< 3\Rightarrow d\) cắt đường tròn tại 2 điểm
c. Khoảng cách giữa 2 điểm trên đường tròn là lớn nhất khi chúng nằm ở 2 mút đường kính
\(\Rightarrow\) d' đi qua tâm I
Do d' vuông góc d nên nhận (1;1) là 1 vtpt
Phương trình: \(1\left(x-2\right)+1\left(y+1\right)=0\Leftrightarrow x+y-1=0\)

Hai đường thẳng Δ1 và Δ2 có vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
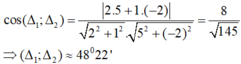
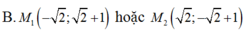
Đường thẳng: 3x + y- 1= 0 có vtpt n 1 =(3;1)
Đường thẳng: 4x -2y -4= 0 có vtpt n 2 =(4;-2)
Chọn B.