K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DL
3
11 tháng 10 2021
\(=\dfrac{1}{\left(5x-1\right)\left(25x^2+5x+1\right)}\)
11 tháng 10 2021
\(\dfrac{1}{125}x^3-1=\left(\dfrac{1}{5}x-1\right)\left(\dfrac{1}{25}x^2+\dfrac{1}{5}x+1\right)\)
NN
1
24 tháng 11 2021
\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)
1 tháng 11 2020
Gọi hóa trị của Nitơ là x. Khi đó: \(N^xO_3^{II}\)
Theo quy tắc hóa trị ta có: x.1=3.II => \(x=\frac{3.II}{1}=VI\)( vô lý)
=> đề?
28 tháng 10 2021
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab==2^2+4\cdot3=16\)
PD
1
AH
Akai Haruma
Giáo viên
19 tháng 9 2021
Lời giải:
$A=11-5x-x^2=11-(x^2+5x)=17,25-(x^2+5x+2,5^2)=17,25-(x+2,5)^2$
Vì $(x+2,5)^2\geq 0$ với mọi $x$ nên $A=17,25-(x+2,5)^2\leq 17,25$
Vậy $A_{\max}=17,25$ khi $x+2,5=0\Leftrightarrow x=-2,5$
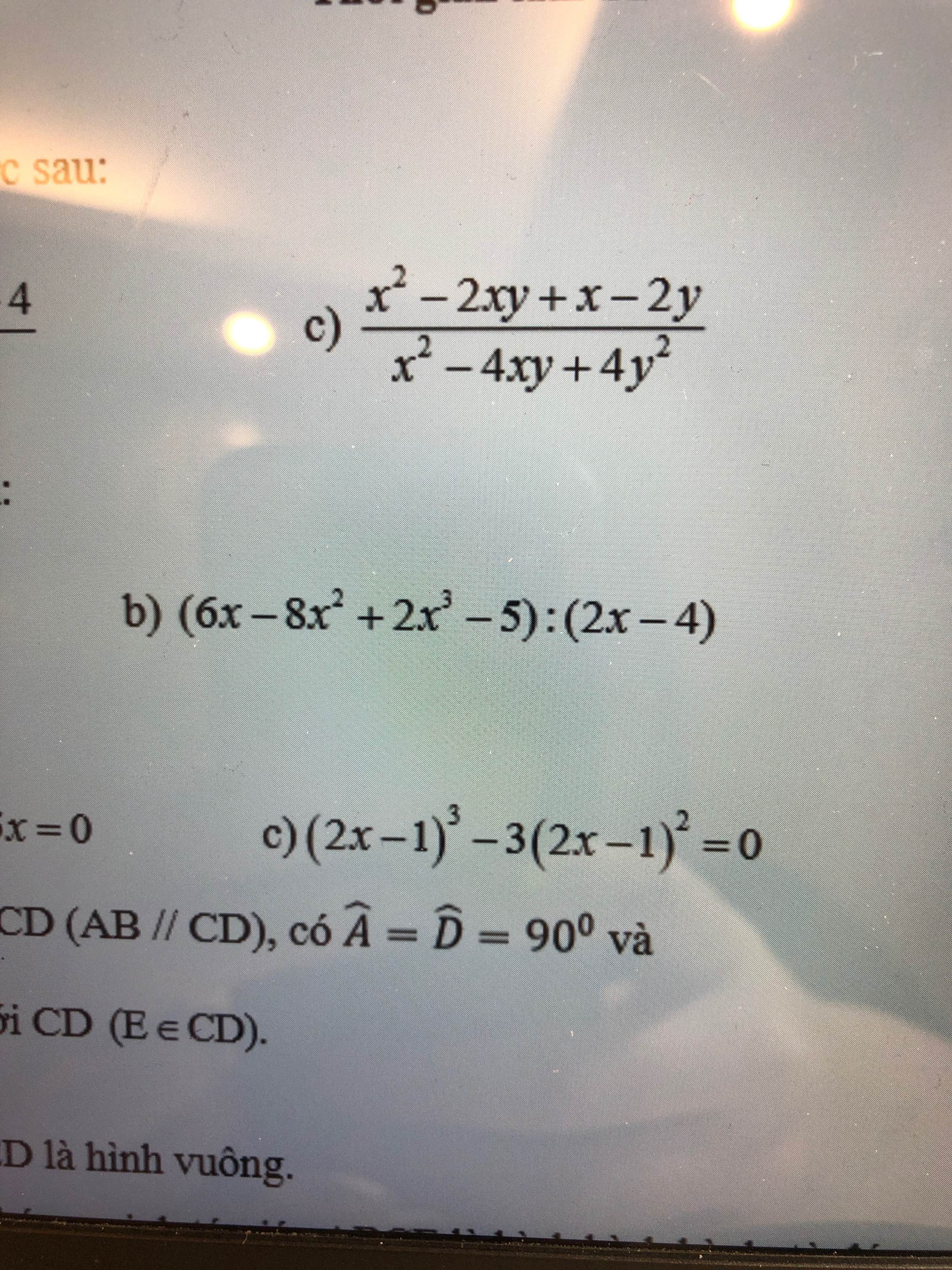
6)
\(\dfrac{3}{2x}+\dfrac{3x-3}{2x-1}+\dfrac{2x^2+1}{4x^2-2x}\)
\(=\dfrac{3}{2x}+\dfrac{3x-3}{2x-1}+\dfrac{2x^2+1}{2x\left(2x-1\right)}\)
\(=\dfrac{3\left(2x-1\right)+\left(3x-3\right).2x+2x^2+1}{2x\left(2x-1\right)}\)
\(=\dfrac{6x-3+6x^2-6x+2x^2+1}{2x\left(2x-1\right)}\)
\(=\dfrac{8x^2-2}{2x\left(2x-1\right)}\)
\(=\dfrac{2\left(4x^2-1\right)}{2x\left(2x-1\right)}\)
\(=\dfrac{2\left(2x+1\right)\left(2x-1\right)}{2\left(2x-1\right)}\)
\(=2x+1\)
Cảm ơn