
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

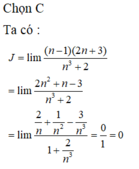

\(a=lim\frac{n^2+n}{6n^3}=lim\frac{\frac{1}{n}+\frac{1}{n^3}}{6}=\frac{0}{6}=0\)
\(b=lim\frac{1+\frac{2}{n}}{1+\frac{1}{n}}+lim\frac{sinn}{2^n}=1+0=1\)
Giải thích: \(-1\le sin\left(n\right)\le1\) \(\forall n\Rightarrow\frac{-1}{2^n}\le\frac{sin\left(n\right)}{2^n}\le\frac{1}{2^n}\)
Mà \(lim\frac{-1}{2^n}=lim\frac{1}{2^n}=0\Rightarrow lim\frac{sin\left(n\right)}{2^n}=0\) theo nguyên tắc giới hạn kẹp
\(c=lim\frac{-3n-1}{\sqrt{n^2-3n}+\sqrt{n^2+1}}=lim\frac{-3-\frac{1}{n}}{\sqrt{1-\frac{3}{n}}+\sqrt{1+\frac{1}{n^2}}}=\frac{-3}{1+1}=-\frac{3}{2}\)
\(d=lim\frac{3n^2}{\sqrt[3]{\left(n^3+3n^2\right)^2}+n\sqrt[3]{n^3+3n^2}+n^2}=lim\frac{3}{\sqrt[3]{\left(1+\frac{3}{n}\right)^2}+\sqrt[3]{1+\frac{3}{n}}+1}=\frac{3}{1+1+1}=1\)