Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a )
tìm ƯCLN của 150,120 và 240
150 = \(2.3.5^2\)
120 =\(2^2.3.5\)
240 =\(2^4.3.5\)
ƯCLN của 150,120 và 240= 2.3.5 = 30
vậy n=30
b)câu b sai đề rồi vì nếu n chia hết cho 150 => n \(\ge\)150.mà 120 chia được cho n khác 0 n≤120 mà lớn hơn 150 và bé hơn 120 với n khác 0 mà ko có số nào như vậy cả vậy nên đề sai
a) Vì 150⋮n, 120⋮n, 240⋮n; n là STN lớn nhất ⇒ n∈ UCLN(150,120,240)
Ta có:
150 = 2.3.52
120 = 2\(^3\).3.5
240 = \(2^4.3.5\)
UCLN (120,150,240)= 2.3.5=30
Vậy...
b) Vì n⋮150, n⋮120, n⋮240; n là STN lớn nhất⇒ n∈ BCNN(150, 120, 240)
Ta có:
150 = 2.3.52
120 = 2\(^3\).3.5
240 = \(2^4.3.5\)
BCNN(150,120,240)= 5\(^2\).\(3.2^4\)= 1200
Vậy...

\(\frac{3n+4}{n-1}\)= \(\frac{3\left(n-1\right)+7}{n-1}\)= 3 + \(\frac{7}{n-1}\)
để A có gt nguyên => n-1 thuộc ước của 7
với n-1 = 7 => n = 8 => A = 4 (nhận)
với n- 1 = -7 => n = -6 => A = 2 (nhận)
với n- 1 = -1 => n= 0 => A = 3 ( nhận)
với n-1 = 1 => n = 2=> A = 3 + \(\frac{7}{2}\)(loại)
Ta có:3n+4/n-1=3n-3+3+4/n-1=3n-3+7/n-1=3n-3/n-1+7/n-1=3n-3x1/n-1+7/n-1=3x(n-1)/n-1+7/n-1=3+7/n-1
Để 3n+4/n-1 hay (3n+4):(n-1) thì 7 chia hết cho (n-1)
=>n-1 thuộc Ư(7) hay n-1 thuộc {-7;-1;1;7}
Với n-1=-7 Với n-1=-1
n =-7+1 n =-1+1
n =-6 n =0
Với n-1=1 Với n-1=7
n =1+1 n =7+1
n =2 n =8
Vậy để 3n+4/n-1 thì n=-6;0;2;8

Lời giải:
$\frac{x}{4}=\frac{18}{x+1}$
$\Rightarrow x(x+1)=18.4$
$x(x+1)=72$
$x(x+1)-72=0$
$x^2+x-72=0$
$(x^2-8x)+(9x-72)=0$
$x(x-8)+9(x-8)=0$
$(x-8)(x+9)=0$
$\Rightarrow x-8=0$ hoặc $x+9=0$
$\Rightarrow x=8$ hoặc $x=-9$
Tập hợp giá trị nguyên của $x$ thỏa mãn điều kiện đề bài là:
$\left\{8; -9\right\}$

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

d: Tổng các số nguyên x thỏa mãn -24<x<18 là:
(-23)+(-22)+(-21)+(-20)+(-19)+(-18)
=-45-41-37=-123


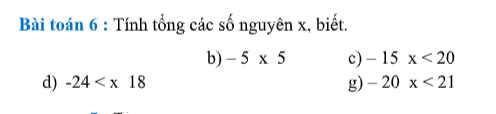
viết còn ngu cơ
Ngu dề "bạn" êi