Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=1\)
\(\Rightarrow a+b=45^0\)

Ta có: \(a^2=b^2+c^2-2bc\cos A\)
\(\Leftrightarrow\cos A=\frac{b^2+c^2-a^2}{2bc}\)
Tương tự: \(\Leftrightarrow\cos B=\frac{a^2+c^2-b^2}{2ac}\)
Ta lại có: \(\frac{a}{\sin A}=\frac{b}{\sin B}=2R\)
\(\left\{\begin{matrix}\sin A=\frac{a}{2R}\\\sin B=\frac{b}{2R}\end{matrix}\right.\)
Quay lại bài toán ta có:
\(\frac{\tan A}{\tan B}=\frac{\sin A\cos B}{\sin B\cos A}=\frac{\frac{a}{2R}.\frac{a^2+c^2-b^2}{2ac}}{\frac{b}{2R}.\frac{b^2+c^2-a^2}{2bc}}=\frac{c^2+a^2-b^2}{c^2+b^2-a^2}\)

\(1=tan\left(\dfrac{\pi}{4}\right)=tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}\)
\(\Rightarrow tana+tanb=1-tana.tanb\)
\(\Rightarrow tana+tanb+tana.tanb=1\)
Do đó:
\(M=1+tana+tanb+tana.tanb=1+1=2\)

Vì A, B, C là ba góc của tam giác nên ta có : A + B + C = π.
⇒ C = π - (A + B); A + B = π - C
a) Ta có: tan A + tan B + tan C = (tan A + tan B) + tan C
= tan (A + B). (1 – tan A.tan B) + tan C
= tan (π – C).(1 – tan A. tan B) + tan C
= -tan C.(1 – tan A. tan B) + tan C
= -tan C + tan A. tan B. tan C + tan C
= tan A. tan B. tan C
b) sin 2A + sin 2B + sin 2C
= 2. sin (A + B). cos (A – B) + 2.sin C. cos C
= 2. sin (π – C). cos (A – B) + 2.sin C. cos (π – (A + B))
= 2.sin C. cos (A – B) - 2.sin C. cos (A + B)
= 2.sin C.[cos (A – B) - cos (A + B)]
= 2.sin C.[-2sinA. sin(- B)]
= 2.sin C. 2.sin A. sin B ( vì sin(- B)= - sinB )
= 4. sin A. sin B. sin C
Tại sao câu b) cái phần sin2A + sin2B lại bằng 2sin(A+B).cos(A-B) vậy ạ

a)\(VT=sinA+sinB+sinC=2sin\frac{A+B}{2}.cos\frac{A-B}{2}+2sin\frac{C}{2}.cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)=4cos\frac{C}{2}.cos\frac{A}{2}.cos\frac{B}{2}\)(đpcm)
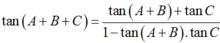
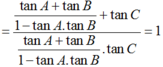
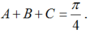

Vì 0<a,b<\(\frac{\pi}{2}\)nên tana,tanb>0 ⇒ tana+tanb>0
ta có tan(a+b)=\(\frac{tana+tanb}{1-tana.tanb}\) ⇔tana+tanb=tan(a+b)(1-3+2\(\sqrt{2}\))
⇔tana+tanb=tan(\(\frac{\pi}{4}\)).(-2+2\(\sqrt{2}\))=-2+2\(\sqrt{2}\)(thỏa)
ta có \(\left\{{}\begin{matrix}tana.tanb=3-2\sqrt{2}\\tana+tanb=-2+2\sqrt{2}\end{matrix}\right.\)
áp đụng hệ thức Vi-et đảo ta có: tana và tanb là hai nghiệm của phương trình: X2+(2-2\(\sqrt{2}\))X+3-2\(\sqrt{2}\)=0
bấm máy giải phương trình trên ta được 2 nghiệm x1,x2
Vậy (tana;tanb)=(x1;x2) hoặc (x2;x1) và tana.tanb=3-2\(\sqrt{2}\)