Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{8^2}\)
\(B< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{7.8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{8}< 1\)
\(B< 1\)
2/ \(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{20}\right)\)
\(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{19}{20}\)
\(B=\dfrac{1\times2\times3\times...\times19}{2\times3\times4\times...\times20}\)
\(B=\dfrac{1}{20}\)
3/ \(A=\dfrac{7}{4}\cdot\left(\dfrac{3333}{1212}+\dfrac{3333}{2020}+\dfrac{3333}{3030}+\dfrac{3333}{4242}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{12}+\dfrac{33}{20}+\dfrac{33}{30}+\dfrac{33}{42}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{3.4}+\dfrac{33}{4.5}+\dfrac{33}{5.6}+\dfrac{33}{6.7}\right)\)
\(A=\dfrac{7}{4}.33.\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}.\left(\dfrac{1}{3}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}\cdot\dfrac{4}{21}\)
\(A=11\)
4/ A phải là \(\dfrac{2011+2012}{2012+2013}\)
Ta có : \(B=\dfrac{2011}{2012}+\dfrac{2012}{2013}>\dfrac{2011}{2013}+\dfrac{2012}{2013}=\dfrac{2011+2012}{2013}>\dfrac{2011+2012}{2012+2013}=A\)
\(\Rightarrow B>A\)

\(A=\dfrac{-10}{3}+\dfrac{19}{6}\cdot\dfrac{7}{5}-\dfrac{19}{3}\cdot\dfrac{1}{10}+\dfrac{19}{10}\cdot\dfrac{4}{3}\)
\(=\dfrac{-10}{3}+\dfrac{19}{3}\cdot\dfrac{7}{10}-\dfrac{19}{3}\cdot\dfrac{1}{10}+\dfrac{19}{3}\cdot\dfrac{4}{10}\)
\(=\dfrac{-10}{3}+\dfrac{19}{3}\cdot\left(\dfrac{7}{10}-\dfrac{1}{10}+\dfrac{4}{10}\right)\)
\(=\dfrac{-10}{3}+\dfrac{19}{3}\cdot\dfrac{10}{10}=\dfrac{-10}{3}+\dfrac{19}{3}\)
\(=\dfrac{9}{3}=3\)

Bài 1)
Ta có:
A = \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+\dfrac{1}{8^2}\)
A < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
A < \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
A < \(1-\dfrac{1}{8}\) = \(\dfrac{7}{8}\) < 1
Vậy A < 1
Bài 2)
Ta thấy:
\(\dfrac{2011}{2012+2013}< \dfrac{2011}{2012};\dfrac{2012}{2012+2013}< \dfrac{2012}{2013}\)
\(\Rightarrow\) \(\dfrac{2011}{2012+2013}+\dfrac{2012}{2012+2013}< \dfrac{2011}{2012}+\dfrac{2012}{2013}\)
\(\Rightarrow\) \(\dfrac{2011+2012}{2012+2013}< \dfrac{2011}{2012}+\dfrac{2012}{2013}\)
\(\Rightarrow\) A < B
Bài 3)
Ta có:
B = \(\left(1-\dfrac{1}{1}\right)\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right)......\left(1-\dfrac{1}{20}\right)\)
= \(0.\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)......\left(1-\dfrac{1}{20}\right)\)
= 0
Bài 3)
Ta có:
A = \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+.....+\dfrac{1}{2^{2012}}\)
\(\Rightarrow\) 2A = \(2\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+.....+\dfrac{1}{2^{2012}}\right)\)
\(\Rightarrow\) 2A = \(2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+.....+\dfrac{1}{2^{2011}}\)
\(\Rightarrow\) 2A - A = \(\left(2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+.....+\dfrac{1}{2^{2011}}\right)\)-\(\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+.....+\dfrac{1}{2^{2012}}\right)\)
\(\Rightarrow\) A = 2 - \(\dfrac{1}{2^{2012}}\) = \(\dfrac{2^{2013}-1}{2^{2012}}\)
Bài 5)
\(\pi\) + 5 \(⋮\) \(\pi\) - 2
\(\Leftrightarrow\) \(\pi\) - 2 + 7 \(⋮\) \(\pi\) - 2
\(\Leftrightarrow\) 7 \(⋮\) \(\pi\) - 2 (vì \(\pi\) - 2 \(⋮\) \(\pi\) - 2)
\(\Leftrightarrow\) \(\pi\) - 2 \(\in\) Ư(7)
\(\Leftrightarrow\) \(\pi\) - 2 \(\in\) \(\left\{\pm1;\pm7\right\}\)
\(\Leftrightarrow\) \(\pi\) \(\in\) \(\left\{1;3;-5;9\right\}\)

\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-16}{10}:\dfrac{5}{3}\)
\(A=\dfrac{-8}{5}.\dfrac{3}{5}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)
\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\dfrac{5}{3}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)

2) Để A là nguyên thì n - 1 là ước nguyên của 2
\(n-1=1\Rightarrow n=2\)
\(n-1=2\Rightarrow n=3\)
3) Ta gọi M là \(\dfrac{12}{5^{2012}}\)
\(M=\dfrac{5.12}{5^{2012}.5}=\dfrac{60}{5^{2013}}\)
\(\Rightarrow\) \(A=\dfrac{60}{5^{2013}}+\dfrac{18}{5^{2013}}=\dfrac{78}{5^{2013}}\)
Ta gọi Q là \(\dfrac{18}{5^{2012}}\)
\(Q=\dfrac{18}{5^{2012}}=\dfrac{18.5}{5^{2012}.5}=\dfrac{90}{5^{2013}}\)
\(\Rightarrow\) \(B=\dfrac{90}{5^{2013}}+\dfrac{12}{5^{2013}}=\dfrac{102}{5^{2013}}\)
\(\dfrac{90}{5^{2013}}< \dfrac{102}{5^{2013}}\Rightarrow A< B\)
Ai thấy đúng thì ủng hộ mink, thấy sai góp ý nha !!!
![]()

Ta có : 2A = \(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2011}}\)
2A - A = \(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2011}}\)- \(\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2012}}\right)\)
A = 2 - \(\dfrac{1}{2^{2012}}\)

Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn,
Với , thì
ĐS. ; C = 0.
Xem thêm tại: http://loigiaihay.com/bai-77-trang-39-phan-so-hoc-sgk-toan-6-tap-2-c41a5943.html#ixzz4eU1fQCGw
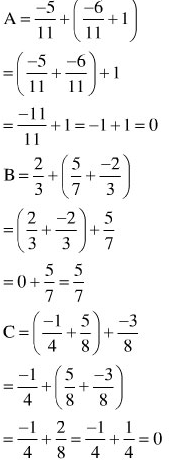
\(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2011}}+\dfrac{1}{2^{2012}}\)
\(\Rightarrow2A=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2011}}\)
\(\Rightarrow2A-A=2-\dfrac{1}{2^{2012}}\)
\(\Rightarrow A=2-\dfrac{1}{2^{2012}}\)
\(A= 1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\)\(\dfrac{1}{2^{2012}}\)
⇒\(2A=2+1+\dfrac{1}{2}+...+\)\(\dfrac{1}{2^{2012}}\)
⇒\(2A-A=(2+1+\dfrac{1}{2}+...+\)\(\dfrac{1}{2^{2012}}\))\(-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2012}}\right)\)
⇒\(A=2-\)\(\dfrac{1}{2^{2012}}\)