
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

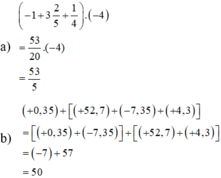

\(a,A=\dfrac{7}{35}+\left(-1\dfrac{3}{4}+\dfrac{12}{7}\right)-\left(\dfrac{1}{4}-\dfrac{2}{7}-\dfrac{12}{35}\right)-\dfrac{3}{7}\)\(A=\dfrac{7}{35}-\dfrac{7}{4}+\dfrac{12}{7}-\dfrac{1}{4}+\dfrac{2}{7}+\dfrac{13}{35}-\dfrac{3}{7}\\ A=\left(\dfrac{7}{35}+\dfrac{13}{35}\right)-\left(\dfrac{7}{4}-\dfrac{1}{4}\right)+\left(\dfrac{12}{7}+\dfrac{2}{7}-\dfrac{3}{7}\right)\)
\(A=\dfrac{4}{7}-\dfrac{3}{2}+\dfrac{11}{7}\\ A=\left(\dfrac{4}{7}+\dfrac{11}{7}\right)-\dfrac{3}{2}\\ A=\dfrac{15}{7}-\dfrac{3}{2}=\dfrac{9}{14}\)

1) a < -1 < 0 => |a| = - a
=> |a| + a = -a + a = 0
2) |7 - 0,35.x| > 0 với mọi x => 4.|7 - 0,35.x| + 8 > 4.0 + 8 = 8
=> GTNN của P của 8 khi 7 - 0,35.x = 0 <=> x = 7: 0,35 = 20
bài làm
Câu1) a < -1 < 0 => |a| = - a
=> |a| + a = -a + a = 0
Câu 2) |7 - 0,35.x| > 0 với mọi x
=> 4.|7 - 0,35.x| + 8 > 4.0 + 8 = 8
=> GTNN của P của 8 khi 7 - 0,35.x = 0
<=> x = 7: 0,35 = 20
hok tốt

1. A = 75(42004 + 42003 +...+ 42 + 4 + 1) + 25
A = 25 . [3 . (42004 + 42003 +...+ 42 + 4 + 1) + 1]
A = 25 . (3 . 42004 + 3 . 42003 +...+ 3 . 42 + 3 . 4 + 3 + 1)
A = 25 . (3 . 42004 + 3 . 42003 +...+ 3 . 42 + 3 . 4 + 4)
A = 25 . 4 . (3 . 42003 + 3 . 42002 +...+ 3 . 4 + 3 + 1)
A =100 . (3 . 42003 + 3 . 42002 +...+ 3 . 4 + 3 + 1) \(⋮\) 100

\(P=\dfrac{2}{3}-\left(-\dfrac{1}{4}\right)+\dfrac{3}{5}-\dfrac{7}{45}-\left(-\dfrac{5}{9}\right)+\dfrac{1}{2}+\dfrac{1}{35}\)
\(P=\dfrac{2}{3}+\dfrac{1}{4}+\dfrac{3}{5}-\dfrac{7}{45}+\dfrac{5}{9}+\dfrac{1}{2}+\dfrac{1}{35}\)
\(P=\left(\dfrac{1}{2}+\dfrac{1}{4}\right)+\left(\dfrac{-7}{45}+\dfrac{2}{3}+\dfrac{5}{9}\right)+\left(\dfrac{3}{5}+\dfrac{1}{35}\right)\)
\(P=\dfrac{3}{4}+\)\(\dfrac{16}{5}\)\(+\dfrac{22}{35}\)
\(P=\dfrac{641}{140}\)
\(P=\dfrac{2}{3}-\left(-\dfrac{1}{4}\right)+\dfrac{3}{5}-\dfrac{7}{45}-\left(-\dfrac{5}{9}\right)+\dfrac{1}{2}+\dfrac{1}{35}\)
\(P=\dfrac{2}{3}+\dfrac{1}{4}+\dfrac{3}{5}-\dfrac{7}{45}+\dfrac{5}{9}+\dfrac{1}{2}+\dfrac{1}{35}\)
\(P=\left(-\dfrac{7}{45}+\dfrac{2}{3}+\dfrac{5}{9}\right)+\left(\dfrac{1}{35}+\dfrac{3}{5}\right)+\left(\dfrac{1}{4}+\dfrac{1}{2}\right)\)
\(P=\left(-\dfrac{7}{45}+\dfrac{30}{45}+\dfrac{25}{45}\right)+\left(\dfrac{1}{35}+\dfrac{21}{35}\right)+\left(\dfrac{1}{4}+\dfrac{2}{4}\right)\)
\(P=\dfrac{48}{45}+\dfrac{22}{35}+\dfrac{3}{4}\)
\(P=\dfrac{1027}{420}\)

\(C=\left[-45^{10}.\left(-5\right)^{10}\right]:75^{10}\)
\(C=\left(-45^{10}.5^{10}\right):75^{10}\)
\(C=\left(-45.5\right)^{10}:75^{10}\)
\(C=\left(-225\right)^{10}:75^{10}\)
\(C=\left(-225:75\right)^{10}=\left(-3\right)^{10}=3^{10}\)
\(B=\left(7^4-7^3\right)^3:343^{12}\)
\(B=\left[7^3.\left(7-1\right)\right]^3:\left(7^3\right)^{12}\)
\(B=\left(7^3.6\right)^3:7^{36}\)
\(B=7^9.6^3:7^{36}\)
\(B=6^3:7^{27}\)