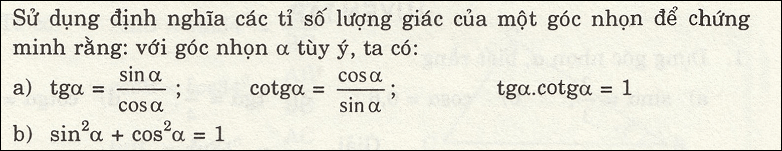Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(cos32=sin58;cos53=sin37;cos8=sin82\)
18<37<44<58<82
=>\(sin18< sin37< sin44< sin58< sin82\)
=>\(sin18< cos53< sin44< cos32< cos8\)
b: 20<45
=>\(sin20< tan20\)
\(cot8=tan82;cot37=tan53\)
20<40<53<82
=>\(tan20< tan40< tan53< tan82\)
=>\(tan20< tan40< cot37< cot8\)
=>\(sin20< tan20< tan40< cot37< cot8\)

Bài 1:
\(\cos60^0=\sin30^0;\sin67^0=\cos23^0;\tan80^0=\cot10^0;\cot20^0=\cot20^0\)
Bài 2:
Xét tam giác ABC vuông tại A
\(a,\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{\dfrac{\sin\alpha}{\cos\alpha}}=\dfrac{\cos\alpha}{\sin\alpha}\\ \tan\alpha\cdot\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\\ b,\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(định.lí.pytago\right)\)

A=(sin220°+sin270°)+(sin230°+sin260°)
+(sin240°+sin250°)-tan245°
=(sin220°+cos220°)+(sin230°+cos230°)+(sin240°+cos240°)-1
=1+1+1-1=2

\(A=s\left(x\right)cs\left(x\right)+\frac{\left(s^3\left(x\right)+cs^3\left(x\right)\right)}{cs\left(x\right)\left(1+t\left(x\right)\right)}=s\left(x\right)cs\left(x\right)+\left(\frac{\left(s\left(x\right)+cs\left(x\right)\right)\left(1-s\left(x\right)cs\left(x\right)\right)}{\left(s\left(x\right)+cs\left(x\right)\right)}\right)\)
\(=1\) vì \(s\left(x\right)+cs\left(x\right)\ne0,\forall0< =x< =\frac{\pi}{2}\)

Ta có: \(\tan^280^o=\tan80^o.\tan80^o=\cot10^o.\cot10^o=\cot^210^o\)
Tương tự: \(\tan^270^o=\cot^220^o\); \(\tan^260^o=\cot^230^o\); \(\tan^250^o=\cot^240^o\)
Thay vào B ta được:
\(B=\tan^210^o.\tan^220^o.\tan^230^o.\tan^240^o.\cot^210^o.\cot^220^o.\cot^230^o.\cot^240^o\)
\(=1^2.1^2.1^2.1^2=1.1.1.1=1\)