Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1)A=a\frac{1}{3}+a\frac{1}{4}-a\frac{1}{6}=a\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)=a\frac{5}{12}\)
Thay \(a=-\frac{3}{5}\) vào A,ta đc:
\(A=-\frac{3}{5}.\frac{5}{12}=-\frac{1}{4}\)
\(2)B=b\frac{5}{6}+b\frac{3}{4}-b\frac{1}{2}=b\left(\frac{5}{6}+\frac{3}{4}-\frac{1}{2}\right)=b\frac{13}{12}\)
Thay \(b=\frac{12}{13}\) vào B, ta đc: \(B=b\frac{13}{12}=\frac{12}{13}.\frac{13}{12}=1\)

A = -4/5x(1/2+1/3+1/4)= -4/5x1 = -4/5
B = 6/19 x ( 3/4+4/3+-1/2)= 6/19x 19 = 6
C = 2002/2003x(3/4+5/6-19/12)=2003/2002x0=0

1)
A = \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+..+\frac{2}{99.101}\)
A = \(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+..+\frac{1}{99}-\frac{1}{101}\)
A = \(\frac{1}{1}-\frac{1}{101}\)
A = \(\frac{100}{101}\)
Vậy A = \(\frac{100}{101}\)
B = \(\frac{5}{1.3}+\frac{5}{3.5}+...+\frac{5}{99.101}\)
B = \(\frac{5}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{99.101}\right)\)
B = \(\frac{5}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\right)\)
B = \(\frac{5}{2}\left(\frac{1}{1}-\frac{1}{101}\right)\)
B = \(\frac{5}{2}.\frac{100}{101}\)
B = \(\frac{250}{101}\)
Vậy B = \(\frac{250}{101}\)
2)
Gọi ƯCLN ( 2n + 1 ; 3n + 2 ) = d ( d \(\in\)N* )
\(\Rightarrow\hept{\begin{cases}2n+1⋮d\\3n+2⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(2n+1\right)⋮d\\2\left(3n+2\right)⋮d\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}6n+3⋮d\\6n+4⋮d\end{cases}\Rightarrow\left(6n+4\right)-\left(6n+3\right)⋮d\Rightarrow1⋮d}\)
\(\Rightarrow d=1\)
Vậy \(\frac{2n+1}{3n+2}\)là p/s tối giản
Gọi ƯCLN ( 2n+3 ; 4n+4 ) = d ( d \(\in\)N* )
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+4⋮d\end{cases}\Rightarrow\hept{\begin{cases}2n+3⋮d\\\left(4n+4\right):2⋮d\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\2n+2⋮d\end{cases}\Rightarrow\left(2n+3\right)-\left(2n+2\right)⋮d}\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vậy ...

a, \(A=\frac{19}{24}-\frac{1}{2}-\frac{1}{3}-\frac{7}{24}=(\frac{19}{24}-\frac{7}{24})-\frac{1}{2}-\frac{1}{3}\)
\(=\frac{12}{24}-\frac{1}{2}-\frac{1}{3}\)
\(=\frac{1}{2}-\frac{1}{2}-\frac{1}{3}=0-\frac{1}{3}=-\frac{1}{3}\)
\(B=\frac{7}{12}+\frac{5}{6}+\frac{1}{4}-\frac{3}{7}-\frac{5}{12}=(\frac{7}{12}-\frac{5}{12})+\frac{5}{6}+\frac{1}{4}-\frac{3}{7}\)
\(=\frac{1}{6}+\frac{5}{6}+\frac{1}{4}-\frac{3}{7}\)
\(=1+\frac{1}{4}-\frac{3}{7}=\frac{23}{28}\)
b, Thay thế A = \(-\frac{1}{3}\)và B = \(\frac{23}{28}\)ta có :
\(-\frac{1}{3}-x=\frac{23}{28}\)
\(\Rightarrow x=-\frac{1}{3}-\frac{23}{28}=-\frac{28}{84}-\frac{69}{84}=\frac{-28-69}{84}=\frac{-97}{84}\)

Bài 1:
a) Ta có: \(\frac{-5}{7}+\frac{2}{7}+\frac{4}{-9}+\frac{4}{9}\)
\(=-\frac{3}{7}+\frac{-4}{9}+\frac{4}{9}\)
\(=-\frac{3}{7}\)
b) Ta có: \(\left(\frac{1}{2}:\frac{3}{4}\right)^2\)
\(=\left(\frac{1}{2}\cdot\frac{4}{3}\right)^2\)
\(=\left(\frac{2}{3}\right)^2=\frac{4}{9}\)
c) Ta có: \(\frac{1}{2}+\frac{3}{4}-\left(\frac{4}{5}+\frac{3}{4}\right)\)
\(=\frac{1}{2}+\frac{3}{4}-\frac{4}{5}-\frac{3}{4}\)
\(=\frac{1}{2}-\frac{4}{5}\)
\(=\frac{5}{10}-\frac{8}{10}=\frac{-3}{10}\)
d) Ta có: \(5^6:5^4+2^3\cdot2^2-225:15^2\)
\(=5^2+2^5-\frac{15^2}{15^2}\)
\(=25+32-1\)
\(=56\)
e) Ta có: \(\frac{7}{23}+\frac{4}{17}-\frac{7}{23}+\frac{13}{17}\)
\(=\frac{4}{17}+\frac{13}{17}\)
\(=\frac{17}{17}=1\)
g) Ta có: \(19\frac{1}{4}\cdot\frac{7}{12}-15\frac{1}{4}\cdot\frac{7}{12}\)
\(=\frac{7}{12}\left(19+\frac{1}{4}-15-\frac{1}{4}\right)\)
\(=\frac{7}{12}\cdot4=\frac{7}{3}\)

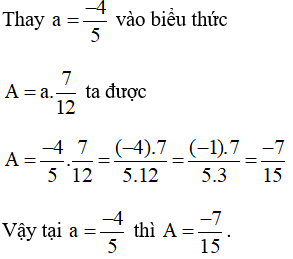



a ,A = \(a.\frac{1}{3}+a.\frac{1}{4}-a.\frac{1}{6}\)
\(=a.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\)
\(=\frac{-3}{5}.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\\ =\frac{-3}{5}.\frac{5}{12}\)
\(=\frac{-1}{4}\)
b, B = \(b.\frac{5}{6}+b.\frac{3}{4}-b.\frac{1}{2}\)
\(=b.\left(\frac{5}{6}+\frac{1}{4}-\frac{1}{2}\right)\)
\(=\frac{12}{13}.\left(\frac{5}{6}+\frac{1}{4}-\frac{1}{2}\right)\)
\(=\frac{12}{13}.\frac{7}{12}\)
\(=\frac{7}{13}\)
a) Thay \(a=\frac{-3}{5}\)vào biểu thức A ta có :
\(A=\frac{-3}{5}.\frac{1}{3}+\frac{-3}{5}.\frac{1}{4}-\frac{-3}{5}.\frac{1}{6}\)
\(A=\frac{-3}{5}.\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\right)\)
\(A=\frac{-3}{5}.\frac{5}{12}\)
\(A=\frac{-1}{4}\)
Vậy giá trị của biểu thức A tại \(a=\frac{-3}{5}\)là \(\frac{-1}{4}\)
b) Thay \(b=\frac{12}{13}\)vào biểu thức B ta có :
\(B=\frac{12}{13}.\frac{5}{6}+\frac{12}{13}.\frac{3}{4}-\frac{12}{13}.\frac{1}{2}\)
\(B=\frac{12}{13}.\left(\frac{5}{6}+\frac{3}{4}-\frac{1}{2}\right)\)
\(B=\frac{12}{13}.\frac{13}{12}\)
\(B=1\)
Vậy giá trị của biểu thức B tại \(b=\frac{12}{13}\)là 1
_Chúc bạn học tốt_