Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S = \(\dfrac{1}{1.4}\)+ \(\dfrac{1}{4.7}\)+...+\(\dfrac{1}{2002.2005}\)
S = ( 1 - \(\dfrac{1}{4}\)+ \(\dfrac{1}{4}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-...+\(\dfrac{1}{2002}\)-\(\dfrac{1}{2005}\)) . \(\dfrac{1}{3}\)
S = ( 1 - \(\dfrac{1}{2005}\)) . \(\dfrac{1}{3}\)
S = \(\dfrac{2004}{2005}\). \(\dfrac{1}{3}\)
S = \(\dfrac{2014}{6015}\)
a) \(S=\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{2002.2005}\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{2002}-\dfrac{1}{2005}\right)\)
\(=\dfrac{1}{3}\left(1-\dfrac{1}{2005}\right)\)
\(=\dfrac{1}{3}.\dfrac{2004}{2005}=\dfrac{668}{2005}\)
KL.
b) \(P=\dfrac{3}{1.6}+\dfrac{3}{6.11}+\dfrac{3}{11.16}+...+\dfrac{3}{96.101}\)
\(=\dfrac{3}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{96}-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{5}\left(1-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{5}.\dfrac{100}{101}=\dfrac{60}{101}\)
KL.
c) \(Q=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{98.99.100}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{98.99}-\dfrac{1}{99.100}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{99.100}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{9900}\right)\)
\(=\dfrac{1}{2}.\dfrac{1}{19800}=\dfrac{1}{39600}\)
KL.

\(S=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+\dfrac{5^2}{11.16}+...+\dfrac{5^2}{96.101}\\ S=\dfrac{25}{1.6}+\dfrac{25}{6.11}+\dfrac{25}{11.16}+...+\dfrac{25}{96.101}\\ S=5.\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+...+\dfrac{5}{96.101}\right)\\ S=5.\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{96}-\dfrac{1}{101}\right)\\ S=5.\left(1-\dfrac{1}{101}\right)\\ S=5.\dfrac{100}{101}\\ S=\dfrac{500}{101}\)

Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn,
Với , thì
ĐS. ; C = 0.
Xem thêm tại: http://loigiaihay.com/bai-77-trang-39-phan-so-hoc-sgk-toan-6-tap-2-c41a5943.html#ixzz4eU1fQCGw

A= \(\dfrac{-3}{5}-\dfrac{-4}{5}+\dfrac{-9}{10}\)
A = \(\dfrac{-7}{10}\)

\(a)\dfrac{-5}{13}+\left(-\dfrac{8}{13}+1\right)\\ =\dfrac{-5}{13}+\dfrac{-8}{13}+1\\ =0+1=1\)
\(b)\dfrac{2}{3}+\left(\dfrac{3}{8}+\dfrac{-2}{3}\right)\\ =\dfrac{2}{3}-\dfrac{2}{3}+\dfrac{3}{8}\\ =\dfrac{3}{8}\)
\(c)\left(\dfrac{-3}{4}+\dfrac{5}{8}\right)+\dfrac{-1}{8}=\dfrac{-3}{4}+\dfrac{4}{8}\\=\dfrac{-6}{8}+\dfrac{4}{8}=\dfrac{-2}{8}=\dfrac{-1}{4}\)

a)
\(P=\dfrac{5}{6}+\dfrac{5}{12}+\dfrac{5}{20}+\dfrac{5}{30}+\dfrac{5}{42}+\dfrac{5}{56}+\dfrac{5}{72}+\dfrac{5}{90}\\ =\dfrac{5}{2.3}+\dfrac{5}{3.4}+\dfrac{5}{4.5}+\dfrac{5}{5.6}+\dfrac{5}{6.7}+\dfrac{5}{7.8}+\dfrac{5}{8.9}+\dfrac{5}{9.10}\\ \Rightarrow\dfrac{1}{5}P=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\\ =\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\\ =\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{5}{10}-\dfrac{1}{10}\\ =\dfrac{4}{10}=\dfrac{2}{5}\\ \Rightarrow P=\dfrac{2}{5}\cdot5=2\)

Ta có: \(B=\left(3\dfrac{10}{99}+4\dfrac{11}{99}-5\dfrac{8}{299}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(B=\left(3\dfrac{10}{99}+4\dfrac{11}{99}-5\dfrac{8}{299}\right)\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\)
\(B=\left(3\dfrac{10}{99}+4\dfrac{11}{99}-5\dfrac{8}{299}\right)\left(\dfrac{3}{6}+\dfrac{-2}{6}+\dfrac{-1}{6}\right)\)
\(B=\left(3\dfrac{10}{99}+4\dfrac{11}{99}-5\dfrac{8}{299}\right)\left(\dfrac{3+\left(-2\right)+\left(-1\right)}{6}\right)\)
\(B=\left(3\dfrac{10}{99}+4\dfrac{11}{99}-5\dfrac{8}{299}\right).0=0\)
Tick mk vs !
B = (3\(\dfrac{10}{99}\)+4\(\dfrac{11}{99}\)-5\(\dfrac{8}{299}\)).0
B = 0

B=\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
B=\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
B=\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
B= 1-\(\dfrac{1}{8}\)
B= \(\dfrac{7}{8}\)
\(A=\dfrac{5}{9}-\dfrac{5}{8}+\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{-3}{8}+\dfrac{1}{3}\\ =\dfrac{5}{9}+\dfrac{-5}{8}+\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{-3}{8}+\dfrac{1}{3}\\= \left(\dfrac{5}{9}+\dfrac{4}{9}\right)+\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\left(\dfrac{-5}{8}+\dfrac{-3}{8}\right)\\ =1+1+\left(-1\right)\\ =2+\left(-1\right)\\ =1\)
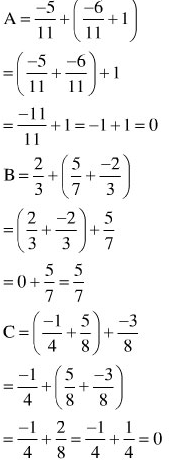
P= \(\dfrac{3}{1.6}\)+\(\dfrac{3}{6.11}\)+\(\dfrac{3}{11.17}\)+...+\(\dfrac{3}{96.101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{5}{3}\).(\(\dfrac{3}{1.6}\)+\(\dfrac{3}{6.11}\)+\(\dfrac{3}{11.16}\)+...+\(\dfrac{3}{96.101}\))
\(\dfrac{5}{3}\).P= \(\dfrac{5}{1.6}\)+\(\dfrac{5}{6.11}\)+\(\dfrac{5}{11.16}\)+...+\(\dfrac{5}{96.101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{1}{1}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{11}\)+\(\dfrac{1}{11}\)-\(\dfrac{1}{16}\)+...+\(\dfrac{1}{96}\)-\(\dfrac{1}{101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{1}{1}\)-\(\dfrac{1}{101}\)= \(\dfrac{101}{101}\)-\(\dfrac{1}{101}\)=\(\dfrac{100}{101}\)
P= \(\dfrac{100}{101}\):\(\dfrac{5}{3}\)= \(\dfrac{100}{101}\).\(\dfrac{3}{5}\)=\(\dfrac{100.3}{101.5}\)=\(\dfrac{20.3}{101.1}\)=\(\dfrac{60}{101}\)
Vậy P= \(\dfrac{60}{101}\)
11.17 chứ không phải 11.16 bạn àk