PD
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QA
2 tháng 8 2021
Trả lời:
1, A = 49 - 14x + x2 - y2
= ( x2 - 14x + 49 ) - y2
= ( x - 7 )2 - y2
= ( x - 7 - y ) ( x - 7 + y )
Thay x = 1; y = - 2 vào A, ta có:
A = [ 1 - 7 - ( - 2 ) ] [ 1 - 7 + ( - 2 ) ]
= ( - 4 ) ( - 8 )
= 32
2, B = 4x - 95 - 6y - 1
Thay x = y = 2 vào B, ta có:
B = 4.2 - 95 - 6.2 - 1
= - 100
2 tháng 8 2021
\(A=49-14x+x^2-y^2=\left(x-7\right)^2-y^2=\left(x-7-y\right)\left(x-7+y\right)\)
Thay x = 1 ; y = -2 ta được : \(-4.\left(-8\right)=32\)
\(B=4x-95-6y-1\)
Thay x = y = 2 ta đươc : \(8-95-12-1=-116\)
31 tháng 7 2021
1)
Thay x=1,y=-2 vào đa thức A có:
49-14.1+1^2+2^2
=49-14+1+4
=40
UB
1
14 tháng 8 2019
\(a,A=4x^2-20x+27=\left(2x\right)^2-2.2x.5+5^2+2\)\(=\left(2x-5\right)^2+2\)
Mà \(\left(2x-5\right)^2\ge0\Rightarrow\left(2x-5\right)^2+2>0\Rightarrow A>0\)
\(b,B=x^2+x+1=x^2+2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}+1\)\(=\left(x-\frac{1}{4}\right)^2+\frac{3}{4}\)
Mà \(\left(x-\frac{1}{4}\right)^2\ge0\Rightarrow\left(x-\frac{1}{4}\right)^2+\frac{3}{4}>0\Rightarrow B>0\)
\(c,C=x^2+4x+y^2-6y+15=x^2+4x+4+y^2-6y+9+2\)
\(\left(x+2\right)^2+\left(y-3\right)^2+2\)
Mà \(\left(x+2\right)^2+\left(y-3\right)^2\ge0\Rightarrow\left(x+2\right)^2+\left(y-3\right)^2+2>0\Rightarrow C>0\)
VP
0
KN
12 tháng 10 2019
2a) \(4x^2-1=\left(2x\right)^2-1^2=\left(2x+1\right)\left(2x-1\right)\)
b) \(x^2+16x+64=\left(x+8\right)^2\)
c) \(x^3-8y^3=x^3-\left(2y\right)^3\)
\(=\left(x-2y\right)\left(x^2+2xy+4y^2\right)\)
d) \(9x^2-12xy+4y^2=\left(3x-2y\right)^2\)
4 tháng 9 2021
\(A=x^2+4x+5=\left(x+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x=-2\)
\(B=x^2+10x-1=\left(x+5\right)^2-26\ge-26\)
Dấu \("="\Leftrightarrow x=-5\)
\(C=5-4x+4x^2=\left(2x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(D=x^2+y^2-2x+6y-3=\left(x-1\right)^2+\left(y+3\right)^2-13\ge-13\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
\(E=2x^2+y^2+2xy+2x+3=\left(x+y\right)^2+\left(x+1\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow x=-y=-1\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
4 tháng 9 2021
\(A=x^2+4x+5\)
\(=x^2+4x+4+1\)
\(=\left(x+2\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi x=-2
\(C=4x^2-4x+5\)
\(=4x^2-4x+1+4\)
\(=\left(2x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
20 tháng 9 2021
2) \(P=\left(2x+1\right)\left(4x^2-2x+1\right)=8x^3+1=8.\left(\dfrac{1}{2}\right)^3+1=8.\dfrac{1}{8}+1=2\)
\(Q=\left(x+3y\right)\left(x^2-3xy+9y^2\right)=x^3+27y^3=1^3+27.\left(\dfrac{1}{3}\right)^3=1+27.\dfrac{1}{27}=2\)
3) \(\left(8x+2\right)\left(1-3x\right)+\left(6x-1\right)\left(4x-10\right)=-50\)
\(\Leftrightarrow-24x^2+2x+2+24x^2-64x+10=-50\)
\(\Leftrightarrow-62x=-62\Leftrightarrow x=1\)
20 tháng 9 2021
Bài 4:
Ta có: \(\left(8x+2\right)\left(1-3x\right)+\left(6x-1\right)\left(4x-10\right)=-50\)
\(\Leftrightarrow8x-24x^2+2-6x+24x^2-60x-4x+40=-50\)
\(\Leftrightarrow-62x=-92\)
hay \(x=\dfrac{46}{31}\)
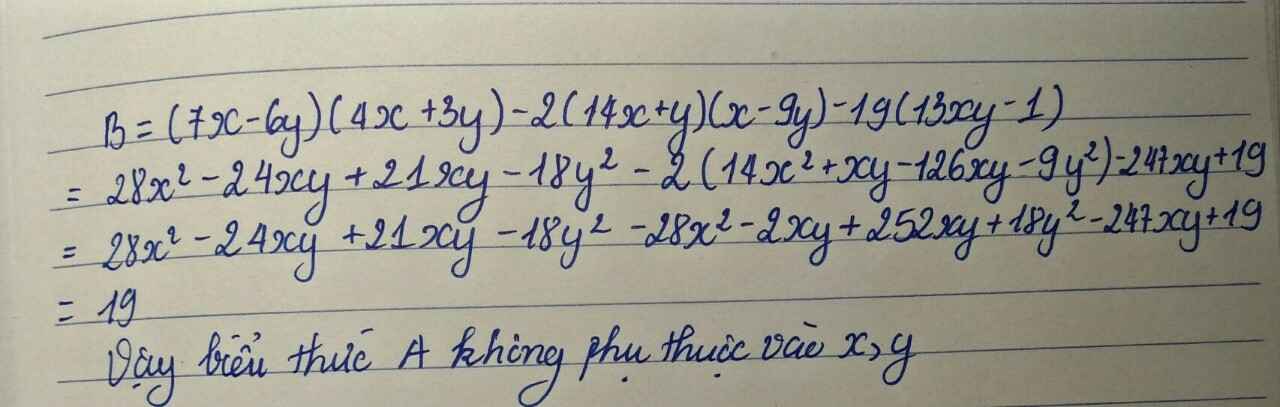
thay x=y=2 vào đa thức B có:
4.2 - 95 - 6.2 - 1
=8-95-12-1
=-100
Vậy...
2, B = 4x - 95 - 6y - 1 tại x = y = 2
B = 4 x 2 - 95 - 6 x 2 - 1
B = 8 - 95 - 12 - 1
B = -100