Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S^2=\left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\\ \text{Ta có:}\\ \dfrac{1}{2}< \dfrac{2}{3}\\ \dfrac{3}{4}< \dfrac{4}{5}\\ \dfrac{5}{6}< \dfrac{6}{7}\\ ...\\ \dfrac{199}{200}< \dfrac{200}{201}\\ \Rightarrow S^2< \left(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot...\cdot\dfrac{199}{200}\right)\left(\dfrac{2}{3}\cdot\dfrac{4}{5}\cdot\dfrac{6}{7}\cdot...\cdot\dfrac{200}{201}\right)\\ \Leftrightarrow S^2< \dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{199}{200}\cdot\dfrac{200}{201}\\ \Leftrightarrow S^2< \dfrac{1\cdot2\cdot3\cdot...\cdot200}{2\cdot3\cdot4\cdot...\cdot201}\\ \Leftrightarrow S^2< \dfrac{1}{201}< \dfrac{1}{200}\)
Vậy ...

\(\left(\dfrac{1}{200}+\dfrac{1}{300}+\dfrac{1}{400}+...+\dfrac{1}{1000}\right).1.2.3.4.5\).\(\left(\dfrac{1}{120}-\dfrac{1}{180}-\dfrac{1}{360}\right)\)
Xét \(\left(\dfrac{1}{120}-\dfrac{1}{180}-\dfrac{1}{360}\right)\) ta có :
= \(\dfrac{1}{120}-\left(\dfrac{1}{180}+\dfrac{1}{360}\right)\) =\(\dfrac{1}{120}-\dfrac{1}{120}=0\)
Trong 1 tích nếu có 1 thừa số 0 thì tích đó bằng 0
Biểu thức trên có 1 thừa số 0 nên biểu thức trên bằng 0

a: =>4x-5=0 hoặc 5/4x-2=0
=>x=5/4 hoặc x=2:5/4=2*4/5=8/5
b: =>(1/12+19/6-30,75)*x-8=102
=>-55/2x=110
=>x=-4

a: A>1/150*50+1/200*50=1/3+1/4=7/12
b: A>7/12
7/12>5/8
=>A>5/8

\(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{199}-\dfrac{1}{200}\)
\(=\left(1+\dfrac{1}{3}+...+\dfrac{1}{199}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+..+\dfrac{1}{200}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{199}+\dfrac{1}{200}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{200}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{199}+\dfrac{1}{200}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{100}\right)\)
\(=\dfrac{1}{101}+...+\dfrac{1}{199}+\dfrac{1}{200}\)

a, \(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{24}\)
= \(\dfrac{28}{15}.\dfrac{25}{100}.3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right):\dfrac{47}{24}\)
= \(\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{32-79}{60}\right).\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-47}{60}.\dfrac{24}{47}\)
= \(\dfrac{84}{60}+\dfrac{-24}{60}=\dfrac{60}{60}=1\)
b, \(\dfrac{\left(\dfrac{11^2}{200}+0,415\right):0,01}{\dfrac{1}{12}-37,25+3\dfrac{1}{6}}\)
= \(\dfrac{\left(\dfrac{121}{200}+\dfrac{415}{1000}\right):\dfrac{1}{100}}{\dfrac{1}{12}-\dfrac{3725}{100}+\dfrac{19}{6}}=\dfrac{\left(\dfrac{121}{200}+\dfrac{83}{200}\right).100}{\dfrac{1}{12}-\dfrac{149}{4}+\dfrac{19}{6}}\)
= \(\dfrac{\dfrac{51}{50}.100}{-34}=\dfrac{102}{-34}=-3\)

Ta có:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\) (có 50 số hạng)
⇔ \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{3}\) \(\left(1\right)\)
\(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+\dfrac{1}{200}+...+\dfrac{1}{200}\) (có 50 số hạng)
⇔ \(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{4}\) \(\left(2\right)\)
Từ (1) và (2), cộng vế theo vế. Ta được:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}+\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
⇒ \(ĐPCM\)

Chứng minh :
\(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{200}< \dfrac{25}{12}\)
Ta có :
\(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{200}\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{200}\right)\)
\(=\dfrac{25}{12}+\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{200}\right)>\dfrac{25}{12}\)

a) \(\dfrac{3}{5}+0,145-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{145}{1000}-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{29}{200}-\dfrac{1}{200}\)
\(=\dfrac{120}{200}+\dfrac{29}{200}-\dfrac{1}{200}\)
\(=\dfrac{148}{200}\)
\(=\dfrac{37}{50}\)
b) \(\left(31\dfrac{6}{13}+5\dfrac{9}{41}\right)-36\dfrac{6}{13}\)
\(=31\dfrac{6}{13}+5\dfrac{9}{41}-36\dfrac{6}{13}\)
\(=\left(31\dfrac{6}{13}-36\dfrac{6}{13}\right)+5\dfrac{5}{41}\)
\(=\left(-5\right)+5\dfrac{5}{41}\)
\(=0\dfrac{5}{41}\)
\(=\dfrac{5}{41}\)
c) \(5.2\dfrac{1}{7}+5.7\dfrac{6}{7}\)
\(=5\left(2\dfrac{1}{7}+7\dfrac{6}{7}\right)\)
\(=5\left(9+\dfrac{1}{7}+\dfrac{6}{7}\right)\)
\(=5\left(9+1\right)\)
\(=5.10\)
\(=50\)
a) \(\dfrac{3}{5}+0,415-\dfrac{1}{200}\)
\(=\dfrac{3}{5}+\dfrac{83}{200}-\dfrac{1}{200}\\ =\dfrac{120}{200}+\dfrac{83}{200}-\dfrac{1}{200}\\ =\dfrac{120+83-1}{200}=\dfrac{202}{200}=\dfrac{101}{100}\)
b)\(\left(31\dfrac{6}{13}+5\dfrac{9}{41}\right)-36\dfrac{6}{13}\)
\(=\left(\dfrac{409}{13}+\dfrac{214}{41}\right)-\dfrac{474}{13}\)
\(=\dfrac{19551}{533}-\dfrac{474}{13}=\dfrac{9}{41}\)
c)\(5.2\dfrac{1}{7}+5.7\dfrac{6}{7}\)
\(=5.\dfrac{15}{7}+5.\dfrac{55}{7}\\ =5\left(\dfrac{15}{7}+\dfrac{55}{7}\right)\\ =5.10=50\)
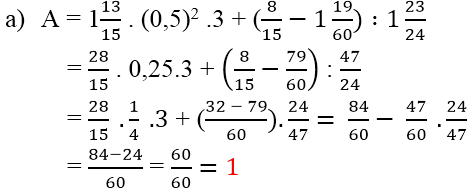
\(P=\dfrac{200}{2}+\dfrac{200}{6}+...+\dfrac{200}{9900}\)
\(=200\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{9900}\right)\)
\(=200\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)
\(=200\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=200\left(1-\dfrac{1}{100}\right)=200\cdot\dfrac{99}{100}=198\)