
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) x≠2x≠2
Bài 2:
a) x≠0;x≠5x≠0;x≠5
b) x2−10x+25x2−5x=(x−5)2x(x−5)=x−5xx2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
c) Để phân thức có giá trị nguyên thì x−5xx−5x phải có giá trị nguyên.
=> x=−5x=−5
Bài 3:
a) (x+12x−2+3x2−1−x+32x+2)⋅(4x2−45

a) Rút gọn E Þ đpcm.
b) Điều kiện xác định E là: x ≠ ± 1
Rút gọn F ta thu được F = 4 Þ đpcm


Điều kiện xác định của phân thức: ax ≠ 0
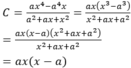
Với 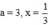 thỏa mãn ĐKXĐ nên thay
thỏa mãn ĐKXĐ nên thay 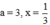 vào biểu thức ta được:
vào biểu thức ta được:
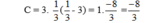

x=7
=>x+1=8
=> A= x^15 - 8x^14 + 8x^13 - 8x^12 +....- 8x^2 + 8x - 5
=x15-(x+1)x14+(x+1)x13-(x+1)x12+...-(x+1)x2+(x+1)x-5
=x15-x15-x14+x14+x13-x13-x12+...-x3-x2+x2+x-5
=x-5
=>A=7-5=2
Vậy A=2 khi x=7
\(B=x^{15}-8x^{14}+8x^{13}-8x^{12}+...+8x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-\left(x+1\right)x^{12}+...+\left(x+1\right)x-x+2\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-x^{13}-x^{12}+...+x^2+x-x+2\)
\(=2\)

a) ĐKXĐ: \(x\ne\pm1\)
b) \(A=\dfrac{x^3-1}{x^2-1}\cdot\left(\dfrac{1}{x-1}-\dfrac{x+1}{x^2+x+1}\right)\left(dkxd:x\ne\pm1\right)\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\left[\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\right]\)
\(=\dfrac{x^2+x+1}{x+1}\cdot\dfrac{x^2+x+1-\left(x^2-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1-x^2+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x+2}{x^2-1}\)
c) Có: \(\left|x+3\right|=1\Leftrightarrow\left[{}\begin{matrix}x+3=1\\x+3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\left(tmdk\right)\)
+) Với \(x=-2\), thay vào \(A\), ta được:
\(A=\dfrac{-2+2}{\left(-2\right)^2-1}=0\)
+) Với \(x=-4\), thay vào \(A\), ta được:
\(A=\dfrac{-4+2}{\left(-4\right)^2-1}=-\dfrac{2}{15}\)
\(\text{#}Toru\)
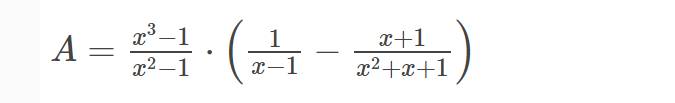
Với a = 13 thì 45 x a = 45 x 13 = 585
Với a = 26 thì 45 x a = 45 x 26 = 1170
Với a = 39 thì 45 x a = 45 x 39 = 1755