DL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 3 2022
Bài 4:
b: \(=x^2z\left(-1+3-7\right)=-5x^2z=-5\cdot\left(-1\right)^2\cdot\left(-2\right)=10\)
c: \(=xy^2\left(5+0.5-3\right)=2.5xy^2=2.5\cdot2\cdot1^2=5\)
26 tháng 8 2023
\(x=7\Rightarrow8=x+1\left(1\right)\)
Thay \(1\) vào \(F\) ta có:
\(F=x^{2006}-\left(x+1\right)^{2005}+\left(x+1\right)^{2004}-...+\left(x+1\right)x^2-\left(x+1\right)x-5\)
\(F=x^{2006}-x^{2006}-x^{2005}+x^{2005}+x^{2004}-...+x^3+x^2-x^2-x-5\)
\(F=-7-5\)
\(\Rightarrow F=-12\)
NA
3
2 tháng 3 2022
\(3x^2-9x=3x\left(x-3\right)\)
Thế x=1 ta được:
\(3.1\left(1-3\right)=3.-2=-6\)
Thế x=\(\dfrac{1}{3}\) ta được:
\(3.\dfrac{1}{3}\left(\dfrac{1}{3}-3\right)=1-\dfrac{8}{3}=-\dfrac{8}{3}\)
PT
1
CM
19 tháng 2 2017
- Thay x = 1 vào biểu thức 3x2 – 9x, ta có:
3.12-9.1 = 3.1 - 9 = 3 - 9 = -6
Vậy giá trị của biểu thức 3x2 – 9x tại x = 1 là – 6
- Thay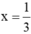 
vào biểu thức trên, ta có:
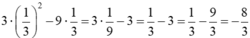
Vậy giá trị của biểu thức 3x2 – 9x tại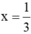 
là 
VD
3
KM
11 tháng 4 2022
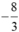
Thay số:
A = 3.(-1).2 - 2.(-1) + 1
A = -3.2 - (-2) + 1
A = -6 + 2 + 1
A = -4 + 1
A = -3
11 tháng 4 2022
Với x = -1 => Ta có:
A=3.2 - 2x + 1
A= 3.2 - 2. (-1) + 1
A= 6 - (-2) +1
A= 6 + 2 + 1
A= 9
CM
13 tháng 4 2019
*Thay x = 1 vào biểu thức ta có:
3.12 – 2.1 – 5 = 3 – 2 – 5 = -4
Vậy giá trị của biểu thức 3x2 – 2x – 5 tại x = 1 là -4.
*Thay x = -1 vào biểu thức ta có:
3.(-1)2 – 2.(-1) – 5 = 3.1 + 2 – 5 = 0
Vậy giá trị của biểu thức 3x2 – 2x – 5 tại x = -1 là 0.
*Thay x = 5/3 vào biểu thức ta có:
5 tháng 7 2023
a)
\(P=\left(x^{14}-9x^{13}\right)-\left(x^{13}-9x^{12}\right)+\left(x^{12}-9x^{11}\right)-...+\left(x^2-9x\right)-\left(x-9\right)+1\)
\(=x^{13}\left(x-9\right)-x^{12}\left(x-9\right)+x^{11}\left(x-9\right)+...+x\left(x-9\right)-\left(x-9\right)+1\)
\(P\left(9\right)=1\)
b)
\(Q=\left(x^{15}-7x^{14}\right)-\left(x^{14}-7x^{13}\right)+\left(x^{13}-7x^{12}\right)-...-\left(x^2-7x\right)+\left(x-7\right)+2\)
\(=x^{14}\left(x-7\right)-x^{13}\left(x-7\right)+x^{12}\left(x-7\right)-...-x\left(x-7\right)+\left(x-7\right)+2\)
\(Q\left(7\right)=2\)
\(3x^2-15x^2+8x^2\)
\(=-4x^2\)
Thay \(x=\dfrac{1}{4}\) vào biểu thức ta được:
\(-4\cdot\left(\dfrac{1}{4}\right)^2=-\dfrac{1}{4}\)
Vậy: ...