Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vật chuyển động chậm dần đều.
Gia tốc vật: \(v^2-v_0^2=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{10^2-15^2}{2\cdot126}=-\dfrac{125}{252}\approx-0,5m/s^2\)
b)Thời gian ô tô chạy thêm được 125m kể từ khi hãm phanh.
\(S=v_0t+\dfrac{1}{2}at^2\Rightarrow126=15t+\dfrac{1}{2}\cdot\left(-\dfrac{125}{252}\right)\cdot t^2\)
\(\Rightarrow\left[{}\begin{matrix}t=50,4s\\t=10,08s\end{matrix}\right.\)
c)Thời gian để ô tô dừng lại: \(v=v_0+at\)
\(\Rightarrow0=15+\left(-\dfrac{125}{252}\right)\cdot t\Rightarrow t=30,24s\)
d)Thời gian xe đi thêm 100m là:
\(S'=v_0t+\dfrac{1}{2}at^2\Rightarrow100=15t+\dfrac{1}{2}\cdot\left(-\dfrac{125}{252}\right)\cdot t^2\)
\(\Rightarrow\left[{}\begin{matrix}t=52,85s\\t=7,63s\end{matrix}\right.\)
Vận tốc lúc này: \(v'^2-v_0^2=2aS'\)
\(\Rightarrow v'=\sqrt{2aS+v_0^2}=\sqrt{2\cdot\left(-\dfrac{125}{252}\right)\cdot100+15^2}\approx11,22m/s\)
Chọn trục tọa độ trùng với quỹ đạo chuyển động thẳng của ô tô, chiều dương của trục hướng theo chiều chuyển động. Chọn mốc thời gian là lúc ô tô bắt đầu hãm phanh.
Theo công thức liên hệ giữa quãng đường đi được với vận tốc và gia tốc trong chuyển động thẳng chậm dần đều:
v2−v02�2-�02 = 2as
Ta suy ra công thức tính gia tốc của ô tô:
Dấu – của gia tốc a chứng tỏ ô tô chuyển động thẳng chậm dần đều có chiều dương đã chọn trên trục tọa độ, tức là ngược chiều với vận tốc ban đầu v0
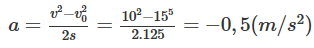
a, \(a=\dfrac{v}{t}=\dfrac{2-1}{5}=0,2\left(m/s\right)\)
b, khi dừng vt=0 \(v_t=v_0+at\)
\(\Leftrightarrow0=10+a.5\Rightarrow a=-2\left(m/s\right)\)