Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)

a)
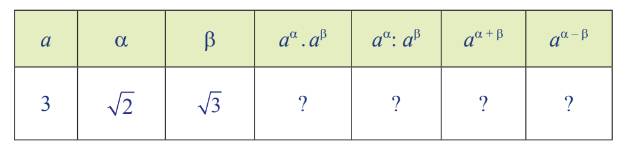
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)

Gọi \({x_1};{x_2};...;{x_{20}}\) là doanh thu bán hàng của các ngày được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2} \in \begin{array}{*{20}{c}}{\left[ {5;7} \right)}\end{array};{x_3},...,{x_9} \in \begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array};{x_{10}},...,{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array};{x_{17}},{x_{18}},{x_{19}} \in \begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array};{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array}\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 7;C = 2 + 7 = 9;{u_j} = 9;{u_{j + 1}} = 11\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 9 + \frac{{\frac{{3.20}}{4} - 9}}{7}.\left( {11 - 9} \right) \approx 10,7\)
Chọn B.

Gọi \({x_1};{x_2};...;{x_{20}}\) là doanh thu bán hàng của các ngày được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2} \in \begin{array}{*{20}{c}}{\left[ {5;7} \right)}\end{array};{x_3},...,{x_9} \in \begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array};{x_{10}},...,{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array};{x_{17}},{x_{18}},{x_{19}} \in \begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array};{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 7;C = 2;{u_m} = 7;{u_{m + 1}} = 9\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7 + \frac{{\frac{{20}}{4} - 2}}{7}.\left( {9 - 7} \right) \approx 7,9\)
Chọn C.

Đặt f ( x ) = x , ta có f’(x) = 1 2 x .
Theo công thức tính gần đúng, với x 0 = 4, ∆ x = -0,01 ta có :
f(3,99) =f(4 – 0,01) ≈ f(4) +f’(4)(-0,01),
tức là 3 , 99 = 4 − 0 , 01 ≈ 4 + 1 2 4 (-0,01)=1,9975
Chọn đáp án A

1 + x 6 = 1 + 6 x + 15 x 2 + 20 x 3 + 15 x 4 + 6 x 5 + x 6 1 , 01 6 = 1 + 0 , 01 6 ≈ 1 + 6 × 0 , 01 + 15 × 0 , 01 2 = 1 , 0615 . b ) D ù n g m á y t í n h t a n h ậ n đ ư ợ c 1 , 01 6 ≈ 1 , 061520151





Ta có 16 , 25 = 16 + 0 , 25 .
Xét hàm số f x = x ⇒ f ' x = 1 2 x
Chọn x0 = 16 và ∆ x = 0,25 , ta có f x 0 + Δ x ≈ f x 0 + f ' x 0 . Δ x
⇒ 16 + 0 , 25 ≈ 16 + 1 2 16 .0 , 25 = 4 + 0 , 03125 = 4 , 03125 ⇒ 16 + 0 , 25 ≈ 4 , 0313
Chọn đáp án A.