
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\sqrt[4]{5}=x\) thì \(x^4=5\). Ta có :
A = \(\frac{2}{\sqrt{4-3x+2x^2-x^3}}\)= \(\frac{2\left(x+1\right)}{\sqrt{\left(x+1\right)^2\left(4-3x+2x^2-x^3\right)}}\)= \(\frac{2\left(x+1\right)}{\sqrt{-x^5+5x+4}}\)
Ta thấy \(-x^5+5x\) = \(x\left(5-x^4\right)\)= \(0\)
nên A = \(\frac{2\left(x+1\right)}{\sqrt{4}}\)= \(x+1\)=\(\sqrt[4]{5}+1\)


\(D=\sqrt{5}-\sqrt{13-4\sqrt{\left(\sqrt{5}-2\right)^2}}=\sqrt{5}-\sqrt{13-4\left(\sqrt{5}-2\right)}\)
\(=\sqrt{5}-\sqrt{21-4\sqrt{5}}=\sqrt{5}-\sqrt{\left(2\sqrt{5}-1\right)^2}\)
\(=\sqrt{5}-2\sqrt{5}+1=1-\sqrt{5}\)
\(B=10\sqrt{5}+\left|1-\sqrt{5}\right|-\frac{4\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=10\sqrt{5}+\sqrt{5}-1-\sqrt{5}+1=10\sqrt{5}\)
\(C=\frac{2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\frac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\frac{12\left(3-\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}\)
\(=\sqrt{3}-1+2+\sqrt{3}+2\left(3-\sqrt{3}\right)=7\)



Đặt \(x=\sqrt[4]{5}\Rightarrow x^4=5\Rightarrow x^4-5=0\)
\(A=\frac{2}{\sqrt{4-3x+2x^2-x^3}}=\frac{2\left(x+1\right)}{\sqrt{\left(x+1\right)^2\left(4-3x+2x^2-x^3\right)}}\)
\(=\frac{2\left(x+1\right)}{\sqrt{4+5x-x^5}}=\frac{2\left(x+1\right)}{\sqrt{4+x\left(5-x^4\right)}}=x+1=\sqrt[4]{5}+1\)
\(B=\left(\frac{-\sqrt[4]{2}\left(1-\sqrt[4]{2}\right)}{1-\sqrt[4]{2}}+\frac{1+\sqrt{2}}{\sqrt[4]{2}}\right)^2-\frac{\sqrt{1+\sqrt{2}+\frac{1}{2}}}{1+\sqrt{2}}\)
\(=\left(-\sqrt[4]{2}+\frac{1}{\sqrt[4]{2}}+\sqrt[4]{2}\right)^2-\frac{\sqrt{3+2\sqrt{2}}}{\sqrt{2}\left(\sqrt{2}+1\right)}\)
\(=\frac{1}{\sqrt{2}}-\frac{\sqrt{\left(\sqrt{2}+1\right)^2}}{\sqrt{2}\left(\sqrt{2}+1\right)}=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=0\)

Bài này nằm trong cuốn nâng cao và phát triển của Vũ Hữu Bình, và lời giải của nó thực sự rất "ảo". Có lẽ trừ tác giả ra, khó ai mà nghĩ được ra cách giải:
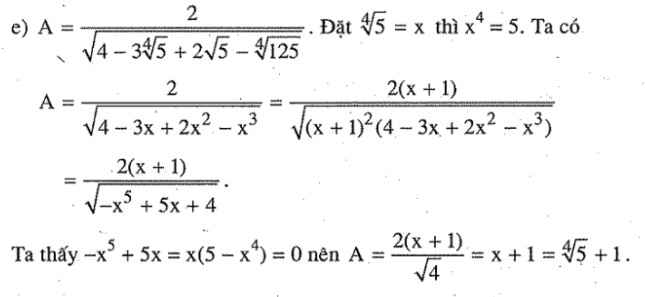
Đặt \(\sqrt[4]{5}=a\)