Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công việc của hàm là thực hiện sắp xếp.
Độ phức tạp của thuật toán là O(n2)

*Chương trình 1:
from collections import Counter
import time
n = 1000
c = 0
# Ghi lại thời điểm bắt đầu
start_time = time.time()
for k in range(n):
c = c + 1
# Ghi lại thời điểm kết thúc
end_time = time.time()
# Tính thời gian hoàn thành
elapsed_time = end_time - start_time
# Sử dụng hàm Counter để đếm số lần lặp
counter = Counter(range(n))
# In số lần lặp
print("Số lần lặp: {}".format(counter))
# In thời gian thực thi
print("Thời gian thực thi của chương trình: {:.6f} giây".format(elapsed_time))
*Chương trình 2:
import time
n = 1000
c = 0
# Ghi lại thời điểm bắt đầu
start_time = time.perf_counter()
for k in range(n):
for j in range(n):
c = c + 1
# Ghi lại thời điểm kết thúc
end_time = time.perf_counter()
# Tính thời gian hoàn thành
elapsed_time = end_time - start_time
# In số lần lặp
print("Số lần lặp: {}".format(c))
# In thời gian thực thi
print("Thời gian thực thi của chương trình: {:.6f} giây".format(elapsed_time))
→Sự khác biệt độ phức tạp thời gian của 2 chương trình trên:
Độ phức tạp thời gian của chương trình 1 là O(1), còn độ phức tạp thời gian của chương trình 2 là O(n2).

Chương trình trên tính số lần lặp cần thiết để i lớn hơn n bằng cách nhân i với 2 trong mỗi lần lặp, sau đó tăng biến sum lên 1. Để xác định độ phức tạp thời gian của chương trình này, ta cần xem xét số lần lặp của vòng while và các phép toán trong vòng lặp.
Vòng while: Vòng lặp này chạy cho đến khi i >= n, và giá trị ban đầu của i là 1. Trong mỗi lần lặp, i được nhân với 2, vậy số lần lặp là log2(n) (vì sau mỗi lần nhân i với 2, giá trị của i sẽ gấp đôi). Ví dụ, nếu n = 1000 thì số lần lặp là log2(1000) ≈ 10.
Các phép toán trong vòng lặp:
Phép gán i = i * 2: Đây là phép nhân, có độ phức tạp là O(1).
Phép gán sum = sum + 1: Đây là phép gán giá trị vào biến sum, có độ phức tạp là O(1).
Vậy tổng độ phức tạp thời gian của chương trình là O(log n), hay O(log2(1000)) ≈ O(10)

Bài 2:
Program HOC24;
var a: array[1..200] of integer;
i,d,n: integer;
begin
write('Nhap so phan tu N: '); readln(N);
for i:=1 to n do
begin
write('a[',i,']='); readln(a[i]);
end;
for i:=1 to n do if a[i] mod 3=0 then d:=d+1;
write('Co ',d,' phan tu chia het cho 3');
readln
end.
Bài 3:
Program HOC24;
var a: array[1..30] of integer;
i,d,n: integer;
begin
write('Nhap so phan tu N: '); readln(N);
for i:=1 to n do
begin
write('a[',i,']='); readln(a[i]);
end;
d:=1;
for i:=1 to n do if a[i] mod 2=0 then d:=d*a[i];
write(Tich cac phan tu chia het cho 2 la: ',d);
readln
end.

THAM KHẢO!
Chương trình trên tính tổng các giá trị i*(i+1) trong khoảng từ 0 đến n-1 và lưu kết quả vào biến s. Để xác định độ phức tạp thời gian của chương trình này, ta cần xem xét số lần lặp của vòng for và các phép toán trong vòng lặp.
Vòng for: Vòng lặp này chạy từ 0 đến n-1, với n là 1.000. Vậy số lần lặp là n, hay 1.000 lần.
Các phép toán trong vòng lặp:
Phép gán s = s + i*(i+1): Đây là phép gán giá trị vào biến s, có độ phức tạp là O(1).
Phép toán i*(i+1): Đây là phép nhân và cộng, có độ phức tạp là O(1).
Vậy tổng độ phức tạp thời gian của chương trình là O(n), hay O(1.000)

1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
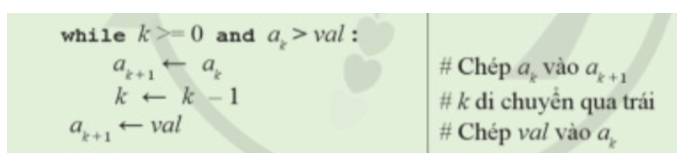
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1

a) T(n) = 2n(n - 2) + 4 = 2n2 - 4n + 4 = O(n2)
b) T(n) = n3 + 5n – 3 = O(n3)