
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi C, D lần lượt là hình chiếu của A, B
Xét △COA vuông tại C có: COA = 45o (gt) => △COA vuông cân tại C => CO = AC => CO2 = AC2
Xét △COA vuông tại C có: OA2 = OC2 + AC2 (định lý Pytago) => OA2 = 2 . OC2 => OA = \(\sqrt{2}\). OC
Xét △OBD vuông tại D có: BOD = 45o (gt) => △OBD vuông cân tại D => OD = BD => OD2 = BD2
Xét △OBD vuông tại D có: OB2 = BD2 + OD2 (định lý Pytago) => OB2 = 2 . OD2 => OB = \(\sqrt{2}\). OD
Ta có: AB = OB - OA => \(\sqrt{2}\)= \(\sqrt{2}\). OD - \(\sqrt{2}\). OC => \(\sqrt{2}\)= \(\sqrt{2}\). CD => CD = 1
Vậy....
@Nhật Hạ : Thực ra trong sách ngta cũng có hướng dẫn giải, nhưng do vắn tắt qua nên mình không thể hiểu nổi.
Có gợi ý như đây : imgur.com/a/vwBcRid
Giải như sau : \(\Delta IAB\)vuông tại I, có \(\widehat{B}=45^o\)nên \(\Delta\)IAB vuông cân suy ra IA = IB
Ta có : AI2 + IB2 = AB2 ; 2AI2 = \(\left(\sqrt{2}\right)^2\)= 2 ; AI2 = 1 do đó HK = 1
Cách giải như này thì có thật sự là quá vắn tắt không nhỉ? Dù sao cũng cảm ơn @Nhật Hạ đã giúp mình

Bài 1 : A B C D 4
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
Bài 2 :
A B C D 3 căn27
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm
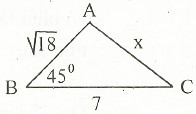
.png)