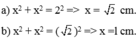TB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 1 2022
a: Gọi độ dài cạnh góc vuông là x
Theo đề, ta có: \(2x^2=4\)
hay \(x=\sqrt{2}\left(cm\right)\)
b: Gọi độ dài cạnh góc vuông là x
Theo đề, ta có: \(2x^2=2\)
hay x=1(cm)
NT
3
5 tháng 4 2018
cạnh huyền của tam giác vuông đó là : căn bậc 2 của ( 2 ^ 2 + 2 ^ 2 ) = 2,83 dm
đáp số : 2,83 dm
21 tháng 4 2020
Gọi cạnh huyền cần tìm là x
Áp dụng định lí Pytago cho tam giác vuông cân trên ta có :
x2 = 22 + 22
x2 = 4 + 4
x2 = 8
=> \(x=\sqrt{8}=2,8284...=2,83dm\)
Vậy cạnh huyền của tam giác đó = 2, 83dm
16 tháng 3 2020
a) Xét \(\Delta ABC\)vuông cân tại A
Áp dụng định lí Pi-ta-go ta có :
\(AB^2+AC^2=BC^2=2^2=4\Rightarrow2AB^2=4\Rightarrow AB^2=2\Rightarrow AB=\sqrt{2}\approx1,4\left(cm\right)\)
b) Xét \(\Delta ABC\)vuông cân tại A
Áp dụng định lí Pitago ta có :
\(AB^2+AC^2=BC^2=\sqrt{2}^2=4\Rightarrow2AB^2=4\Rightarrow AB^2=2\Rightarrow AB=\sqrt{2}\approx1,4\left(cm\right)\)
Câu a,b đều giống nhau cả :))
\(\sqrt{2}cm\)chứ không phải \(\sqrt{2cm}\)
17 tháng 3 2020
Câu b để mình sửa lại nhé,mình nhầm trầm trọng
Thông cảm cho mk :))
b) Xét \(\Delta ABC\)vuông tại A có :
\(AB^2+AC^2=BC^2=\sqrt{2}^2=2\Rightarrow2AB^2=2\Rightarrow AB^2=1\Rightarrow AB=1\left(cm\right)\)
=> Độ dài cạnh góc vuông là 1cm.
TD
2
KK
3 tháng 1 2017
vì tam giác đó là tam giác vuông cân nên 2 cạnh góc vuông bằng nhau
Gọi cạnh huyền của tam giác đó là x
Theo định lý Pytago ta có: x2 = 22 + 22
x2 = 4 + 4
x2 = 8
x = căn 8
mk ko có máy tính nên bạn tự tính nhé
14 tháng 1 2017
Bài này dễ thế mà mi góp ý là những câu hỏi dễ như thế này bạn nên tự suy luận vì kiến thức thầy cô đã dạy hết rồi
PT
1
CM
25 tháng 12 2019
Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)
Áp dụng định lí pitago ta có:
x2 + x2 = 22 => 2x2 = 4 => x2 =2. Do đó x = √2cm