Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ý bạn là tam giác vuông cân?
a) Có tam giác ABC vuông cân, BC là cạnh huyền
Theo BĐT tam giác, AB+AC>BC
Mà AB=AC
=> AB=AC lớn hơn hoặc bằng 2
Khi đó AB+AC=4>BC=2
b) Mình không hiểu bạn nói gì luôn.

a) Xét \(\Delta ABC\)vuông cân tại A
Áp dụng định lí Pi-ta-go ta có :
\(AB^2+AC^2=BC^2=2^2=4\Rightarrow2AB^2=4\Rightarrow AB^2=2\Rightarrow AB=\sqrt{2}\approx1,4\left(cm\right)\)
b) Xét \(\Delta ABC\)vuông cân tại A
Áp dụng định lí Pitago ta có :
\(AB^2+AC^2=BC^2=\sqrt{2}^2=4\Rightarrow2AB^2=4\Rightarrow AB^2=2\Rightarrow AB=\sqrt{2}\approx1,4\left(cm\right)\)
Câu a,b đều giống nhau cả :))
\(\sqrt{2}cm\)chứ không phải \(\sqrt{2cm}\)
Câu b để mình sửa lại nhé,mình nhầm trầm trọng
Thông cảm cho mk :))
b) Xét \(\Delta ABC\)vuông tại A có :
\(AB^2+AC^2=BC^2=\sqrt{2}^2=2\Rightarrow2AB^2=2\Rightarrow AB^2=1\Rightarrow AB=1\left(cm\right)\)
=> Độ dài cạnh góc vuông là 1cm.

Gọi độ dài hai cạnh góc vuông lần lượt là a,b
Theo đề, ta có: a/5=b/12=k
=>a=5k; b=12k
a^2+b^2=52^2
=>169k^2=52^2
=>k=4
=>a=20; b=48

a) Gọi \(\Delta\)ABC vuông cân tại A có BC = 2 cm
Áp dụng định lý Pytago cho \(\Delta\)ABC vuông cân tại A ta có :
AB2 + AC2 = BC2
AB2 + AB2 = 2 ( Vì AB = AC)
2.AB2 = 4
=> AB2 = 2
=> AB = \(\sqrt{2}\)
Vậy AB = AC = \(\sqrt{2}\)(cm)
b) Gọi \(\Delta\)KFC vuông cân tại K có FC = \(\sqrt{2}\)(cm)
Áp dụng định lý Pytago cho \(\Delta\)KFC vuông cân tại K ta có :
FC2 = KF2 + KC2
(\(\sqrt{2}\))2 = 2. KF2 (vì KC = KF)
=> 2 = 2 . KF2
=> KF2 = 1
=> KF = 1 (cm)
Vậy KC = KF = 1 (cm)

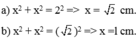

a) Áp dụng định lý Pytago ta có:
x2+x2=22⇒2x2=4⇒x2=2⇒x=√2
b) Áp dụng định lý Pytago, ta có:
x2+x2=(√2)2
2x2=2⇒x2=1⇒x=1(cm)
2 câu cuối làm tương tự nhé e
Chúc em học tốt