
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


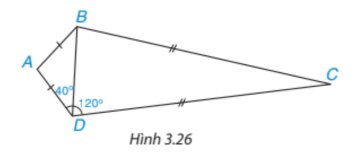
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

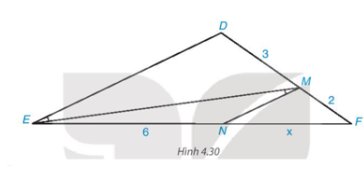
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

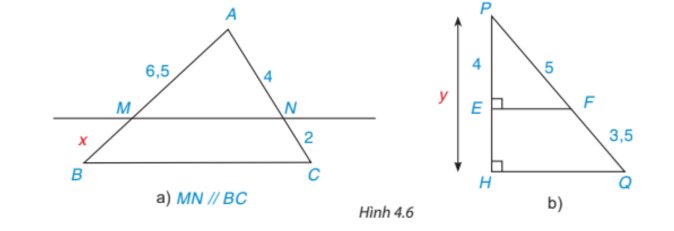
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`

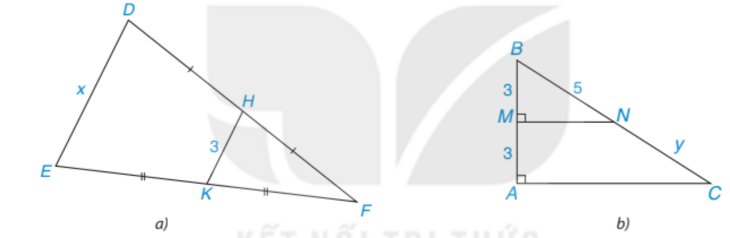
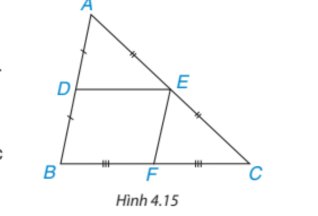
a. Do H, K lần lượt là trung điểm cạnh DF, EF
⇒ HK là đường trung bình của tam giác DEF.
⇒ DE = 2 HK = 2 \(\times\) 3 = 6.
b. Do M là trung điểm cạnh AB mà MN // AC (cùng vuông góc với AB)
⇒ MN là đường trung bình của tam giác ABC.
⇒ N là trung điểm của cạnh BC
⇒ y = NB = NC = 5.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

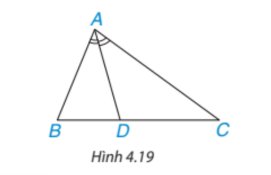
Dựa vào tính chất đường phân giác trong tam giác với tam giác ABC có AD là phân giác của góc \(\widehat{BAC}\) , ta được: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).


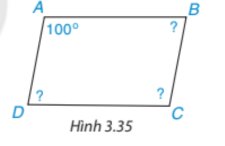
Vì ABCD là hình bình hành nên: \(\widehat A = \widehat C;\widehat B = \widehat D\) ta có:
\(\begin{array}{l}\widehat A = \widehat C = {100^o}\\\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\{100^o} + \widehat B + {100^o} + \widehat B = {360^o}\\2\widehat B + {200^o} = {360^o}\end{array}\)
Suy ra: \(2\widehat B = {360^o} - {200^o} = {160^o}\)
Do đó: \(\widehat B = {80^o}\) suy ra: \(\widehat B = \widehat D = {80^o}\)
Vậy các góc của hình bình hành ABCD là: \(\widehat A = {100^o};\widehat C = {100^o};\widehat B = {80^o};\widehat D = {80^o}\)

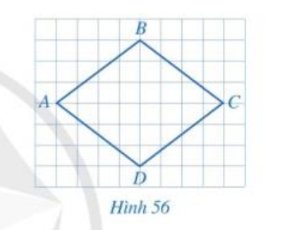
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).





Gọi \(x\) là độ cao của con diều so với mắt nhìn của người (m)
Áp dụng định lý Pythagore vào tam giác vuông trên hình ta có:
\(x^2+25^2=50^2\\ x^2=50^2-25^2=1875\\ x=\sqrt{1875}\approx43,3\left(m\right)\)
Chiều cao của con diều so với mặt đất là:
\(43,3+1=44,3\left(m\right)\)
BC^2=AB^2+AC^2
=>BC=căn 1875(m)
Độ cao của con diều so với mặt đất la:
1+căn 1875\(\simeq\)44,3(m)