Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


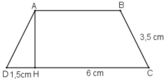
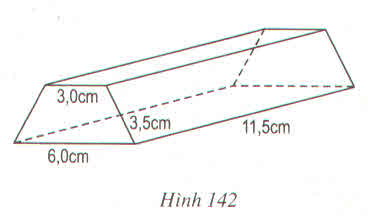
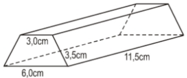
Thanh gỗ dạng hình lăng trụ đứng, đáy là hình thang cân. Ta tìm chiều cao của hình thang cân. Ta có:


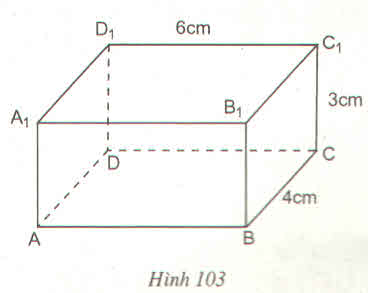
\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)

a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)

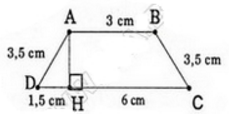
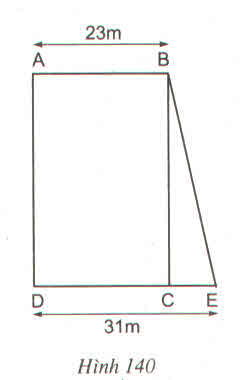
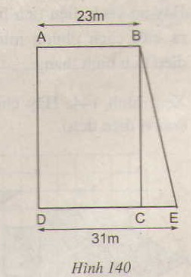
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)

Tham khảo:
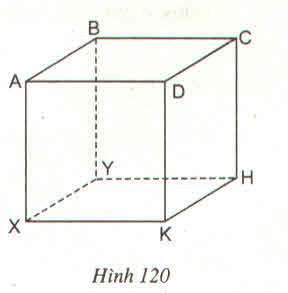
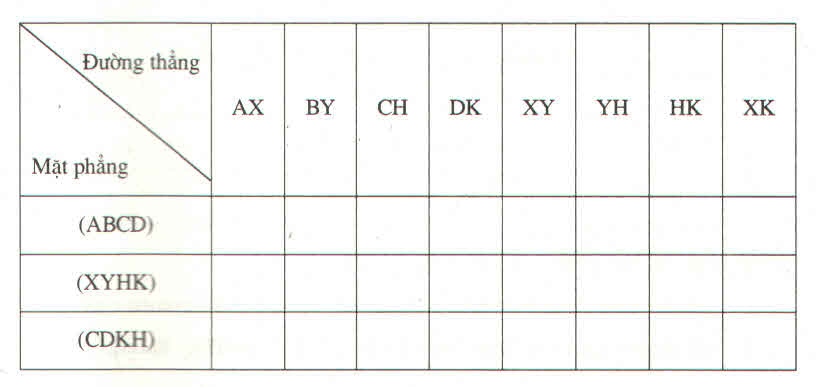
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
d: 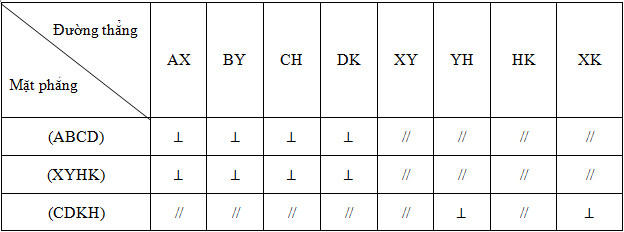

a) Diện tích đáy của hình chóp đều:
S = BC 2 = 6,52 = 42,25 (m2)
Thể tích hình chóp đều:
V = \(\dfrac{1}{3}\). S.h = \(\dfrac{1}{3}\). 42,25 . 12 ≈ 169 (cm3)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5cm. Nên:
Sxq = \(4.\dfrac{\left(2+4\right).3,5}{2}=42\left(cm^2\right)\) = 42 (cm2)