KW
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
UT
4 tháng 4 2021
tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)
4 tháng 4 2021
b) Ta có: HB+HC=BC(H nằm giữa B và C)
nên BC=4+9=13(cm)
Xét ΔBAC có AH là đường cao ứng với cạnh CB(gt)
nên \(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{6\cdot13}{2}=39\left(cm^2\right)\)
4 tháng 4 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Vậy: Độ dài đường cao là AH=6cm
4 tháng 4 2021
a)Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Vậy: AH=6cm
2 tháng 4 2021
a) Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA\(\sim\)ΔHAC(g-g)
CM
7 tháng 9 2019
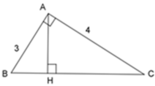
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
8 tháng 3 2021
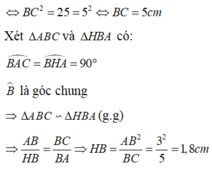
a) Xét ΔABI vuông tại I và ΔACK vuông tại K có
\(\widehat{BAI}\) chung
Do đó: ΔABI\(\sim\)ΔACK(g-g)
26 tháng 7 2018
a.Áp dụng hệ thức h^2=b'.c' vào tam giác vuông ABC ta có: AH^2=HB.HC(đpcm)
AH^2=HB.HC suy ra AH^2=1,8.3,2 suy ra AH^2=5,76 suy ra AH=2,4
S tam giác ABC=1/2 AH.(HB+HC)=1/2.2,4.5=6
PN
1
11 tháng 7 2021
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=\dfrac{12^2}{16}=\dfrac{144}{16}=9\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+9^2=225\)
hay AC=15(cm)
ho tgiác có độ dài các cạnh là a, b, c
độ dài 3 đường cao tương ứng với cạnh a, b, c là ha, hb, hc
độ dài 3 trung tuyến tương ứng với các cạnh a, b, c là ma, mb, mc
độ dài các phân giác trong.. là la, lb, lc
(nhớ ha, hay ma là kí hiệu chứ không phải phép nhân nhé)
-----------------
** đình lí trung tuyến:
4(ma)² + a² = 2b² + 2c² (1)
4(mb)² + b² = 2c² + 2a² (2)
4(mc)² + c² = 2a² + 2b² (3)
lấy (1) + (2) + (3)
4(ma)² + 4(mb)² + 4(mc)² = 3a² + 3b² + 3c²
=> (8/3)[(ma)² + (mb)² + (mc)²] = 2a² + 2b² + 2c² (4)
lần lượt lấy (4) trừ (1), (2), (3) ta sẽ tính được a, b, c theo các trung tuyến
------------------------
Công thức Herong: tính diện tích theo a,b,c với p là nửa chu vi: p = (a+b+c)/2
S = √p(p-a)(p-b)(p-c)
làm tường minh là:
S = (1/4)√(a+b+c)(b+c-a)(c+a-b)(a+b-c)
S = (1/2)a.ha = (1/2)b.hb = (1/2)c.hc
=> a = 2S/ha; b = 2S/hb; c = 2S/hc
thay S từ công thức herong....
----------------
Công thức phân giác:
(la)² = 4bc.p(p-a)/(b+c)² = bc(b+c-a)(a+b+c)/(b+c)²
(lb)² = ...
bạn tự ghi theo cái "khuôn" nhứ thế nhé
-------------------
Vì yêu cầu tính với các cạnh nên chịu dài lê thê như thế, nếu có đựoc một góc thì nhẹ hơn nhiều..
hơn nữa các công thức tôi ghi hầu hết là "ngược", muốn tính lại độ dài các cạnh thì chịu khó giải phương trình
Và hiễn nhiên các công thức trên đều có thể chứng minh, nhưng ghi cái cm ra là chắc chết... hic hic
trong mọi tình huống giải tam giác bạn nên luôn nhớ đến các công thức tính diện tích, để liên kết chúng với nhau
S = (1/2) a.ha = (1/2)b.hb = (1/2)c.hc
= (1/2)bc.sinA = (1/2)ac.sinB = (1/2)ab.sinC
= abc/4R
= pr
= công thức nổi tiếng: Herong
chúc bạn thành công
----------------
Nguồn:__|trituyet|__
\(S=\frac{1}{2}.ha.\left(ha+hc\right)\)