Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(BH+HC=BC\)
\(\Leftrightarrow AH\cdot\cot B+AH\cdot\cot C=BC\)
\(\Leftrightarrow AH\cdot\left(\frac{\sqrt{3}}{3}+1,3\right)=BC\)
\(\Leftrightarrow AH\cdot1,9=10\)
\(\Rightarrow AH=5,3\left(cm\right)\)
\(\Rightarrow AC=\frac{AH}{\sin C}=\frac{5,3}{0,6}=8,2\left(cm\right)\)
b) Ta có: \(S_{ABC}=\frac{AH\cdot BC}{2}=\frac{5,3\cdot10}{2}=26,5\left(cm^2\right)\)
P/s: Các kết quả chỉ tương đối

\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
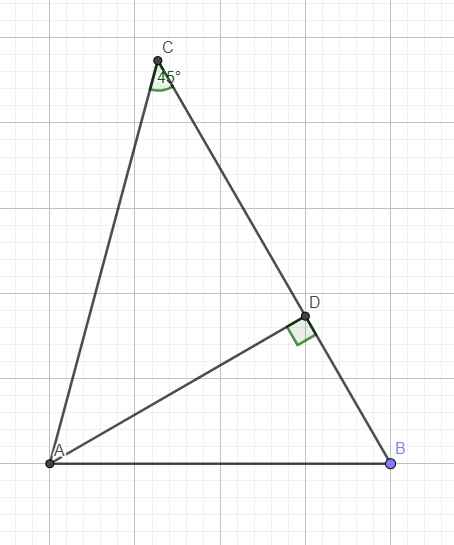
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)

Áp dụng hàm số sin, ta có: \(\frac{a}{\sin A}+\frac{b}{\sin B}+\frac{c}{\sin C}=\frac{a+b+c}{\sin A+\sin B+\sin C}\)
\(\Rightarrow b=\frac{\left(a+b+c\right).\sin B}{\sin A+\sin B+\sin C}\)
\(AH=b\sin C=\frac{\left(a+b+c\right)\sin B.\sin C}{\sin A+\sin B+\sin C}\)
\(\Leftrightarrow AH=\frac{58.\sin58^o20'.\sin82^o35'}{\sin58^o20'+\sin82^o35'+\sin\left(180^o-58^o20'-82^o35'\right)}\approx19,79288\)

kẻ đường cao AH
tg B =AH/HB=>HB=AH/tg B
tg C=AH/CH => CH=AH/tg C
ta có HB+HC=AH/tg B +AH/tg C hay AH(1/tg40*+1/tg55*)=40
=> AH=21,1421(kết quả gần đúng)
diện tích tam giác ABC = (AH.BC)/2 =422,842