Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)

a)Ta có E là trung điểm của CM (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) EF là đường trung bình của (định nghĩa đường trung bình của tam giác)
\(\Rightarrow\) EF//MB (tính chất đường trung bình của tam giác)
hay EF//AB
lại có K là trung điểm của AD (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) KF là đường trung bình của (...)
\(\Rightarrow\) KF//AM (t/c ...)
hay KF//AB
nên EF//KF (vì cùng // với AB)
\(\Rightarrow\) tứ giác EFFIK là hình thang (Định nghĩa hình thang)
Gọi N là trung điểm của AM, nối KM
Ta có N là trung điểm của AM (cách dựng)
K là trung điểm của AD (gt)
\(\Rightarrow\) NK là đường trung bình của
nên NK//DM (t/c....)
mà EN là đường trung bình của (E,I là trung điểm của MC,AM)
\(\Rightarrow\) EI//AC (t/c...)
lại có và
là những tam giác đều (gt)
\(\Rightarrow\)
\(\Rightarrow\) AC//DM
tức là NK//EN (cùng //AC//DM)
do đó 3 điểm E,K,N thẳng hàng (theo tiên đề Ơ-clit)
(2góc đồng vị của AC//EN)
(2 góc đồng vị của KF//AM)
nên
C/m tương tự, lấy P là trung điểm của BM ta cũng được
Hình thang EFIK có
Vậy EFIK là hình thang cân (dấu hiệu nhận biết)
b) Ta có EFIK là hình thang cân (kq câu a)
\Rightarrow EI=KF (tính chất 2 đường chéo trong hình thang cân)
E là trung điểm của CM, I là trung điểm của DM (gt)
\(\Rightarrow\) EI là đường trung bình của tam giác CMD
\(\Rightarrow\) EI=
Vậy KF=

Hình vẽ thế này đúng ko:
A B D E C 23 cm 31 cm
Ta có: \(S_{ABCD}=AB.AD=828m^2\)
Nên \(AD=\frac{828}{23}=36\left(m\right)\)
Do đó diện tích của hình thang ABED là:
\(S_{ABED}=\frac{\left(AB+DE\right).AD}{2}=\frac{\left(23+31\right).36}{2}=972\left(m^2\right)\)


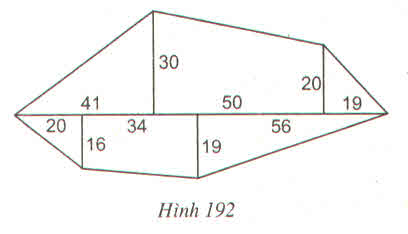
S1=\(\dfrac{30.41}{2}=615\left(cm^2\right)\)
S2=\(\dfrac{\left(30+20\right).50}{2}=1250\left(cm^2\right)\)
S3=\(\dfrac{19.20}{2}=190\left(cm^2\right)\)
S4=\(\dfrac{19.56}{2}=532\left(cm^2\right)\)
S5=\(\dfrac{\left(19+16\right).34}{2}=595\left(cm^2\right)\)
S6=\(\dfrac{16.20}{2}=160\left(cm^2\right)\)
=> S= S1 + S2 +S3 +S4 +S5 +S6= 615+1250+190+532+595+160=3342(m2)

Bài 1)
a) Tứ giác AIHK có 3 góc vuông \(\widehat{HKA}=\widehat{HIA}=\widehat{KAI}=90^0\)
Nên suy ra góc còn lại cũng vuông.Tứ giác có 4 góc vuông là hình chữ nhật
b) Câu này không đúng rồi bạn
Nếu thực sự hai tam giác kia đồng dạng thì đầu bài phải cho ABC vuông cân
Vì nếu góc AKI = góc ABC = 45 độ ( IK là đường chéo đồng thời là tia phân giác của hình chữ nhật)
c) Ta có : Theo hệ thức lượng trong tam giác ABC vuông
\(AB^2=BC.BH=13.4\)
\(\Rightarrow AB=2\sqrt{13}\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\)
Vậy \(S_{ABC}=\frac{AB\cdot AC}{2}=\frac{6\cdot13}{2}=39\left(cm^2\right)\)
Bài 2)
a) \(ED=AD-AE=17-8=9\)
Xét tỉ lệ giữa hai cạnh góc vuông trong hai tam giác ABE và DEC ta thấy
\(\frac{AB}{AE}=\frac{ED}{DC}\Leftrightarrow\frac{6}{8}=\frac{9}{12}=\frac{3}{4}\)
Vậy \(\Delta ABE~\Delta DEC\)
b) \(\frac{S_{ABE}}{S_{DEC}}=\frac{AB\cdot AE\cdot\frac{1}{2}}{DE\cdot DC\cdot\frac{1}{2}}=\frac{6\cdot8}{9\cdot12}=\frac{4}{9}\)
c) Kẻ BK vuông góc DC.Suy ra tứ giác ABKD là hình chữ nhật vì có 4 góc vuông
Nên BK = AD và AB = DK
\(\Rightarrow KC=DC-DK=12-6=6\)
Theo định lý Pytago ta có
\(BC=\sqrt{BK^2+KC^2}=\sqrt{17^2+6^2}=5\sqrt{13}\)

A B C D E F H G L M N P
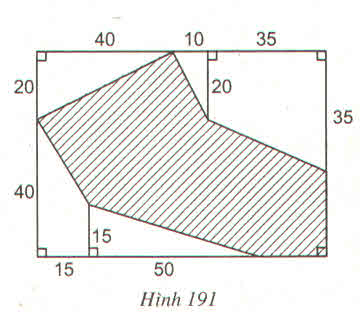
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.

Ta có:
SABCD=(40+10+35).(20+40) = 5100 (cm2)
S1=\(\dfrac{40.20}{2}=400\left(cm^2\right)\)
S2=\(\dfrac{10.20}{2}=100\left(cm^2\right)\)
S3=\(\dfrac{\left(20+35\right).35}{2}=962,5\left(cm^2\right)\)
S4=\(\dfrac{50.15}{2}=375\left(cm^2\right)\)
S5=\(\dfrac{\left(15+40\right).15}{2}=412,5\left(cm^2\right)\)
=> Shình gạch sọc= S - ( S1+S2+S3+S4+S5)= 5100-(400+100+962,5+375+412,5)=2850(cm2)

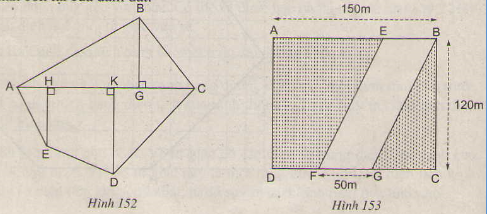
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
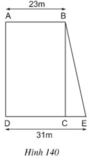
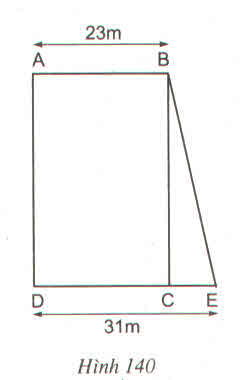
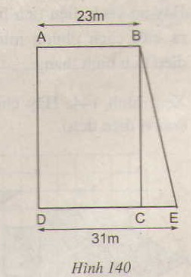


Ta có: SABCD = 828m2
⇔ AD.AB = 828
Mà AB = 23m ⇒ AD = 36m.
Diện tích hình thang ABED là: