Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C B A D 7cm 9cm 8cm 30 độ H
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}\).(7+9).4=32 cm2
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}.\left(7+9\right).4\)=32 cm2

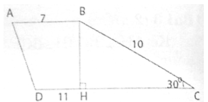
Giả sử hình thang ABCD (AB // CD) có AB = 7cm, BC = 10cm, CD = 11cm và
Kẻ BH ⊥ CD (H ∈ CD) Tam giác BHC vuông tại H lại có ∠C = 30o nên tam giác BHC là nửa tam giác đều. Suy ra
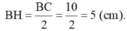
Diện tích hình thang ABCD là:
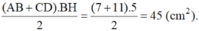

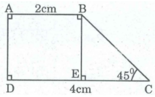
Giả sử hình thang vuông ABCD có:
∠ A = ∠ D = 90 0 ; ∠ C = 45 0
Kẻ BE ⊥ CD
Tam giác vuông BEC có ∠ (BEC) = 90 0 cân tại E ⇒ BE = EC
Hình thang ABCD có hai cạnh bên AD // BE (vì cùng vuông góc với DC) ⇒ DE = AB = 2cm
EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm ( vì tam giác BEC là tam giác vuông cân).
SABCD = 1/2 .BE(AB+ CD) = 1/2 .2.(2 + 4) = 6 ( c m 2 )