Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

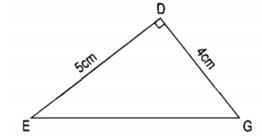
Dt hình thang là
(4+6)×4÷2=20 cm2
Dt hình thang thật là
20×1000=20000 cm2
Đổi 20000cm2 = 2 m2
Bài giải
Độ dài thật của đáy lớn là:
6 x 1000= 6000 (cm)
6000cm= 60m
Độ dài thật của đáy bé là:
4 x 1000= 4000 (cm)
4000cm= 40m
Độ dài thật của chiều cao là:
4 x 1000= 4000
4000cm= 40m
Diện tích thực mảnh đất hình thang là:
\(\frac{\left(40+60\right)\times40}{2}\)= 2000 (m2)
Đ/S: 2000m2.

Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
Đ s:
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2

25cm = 2,5dm
40cm = 4dm
50cm = 5dm
Thể tích của bể cá là :
\(2,5\cdot4\cdot5=50(dm^3)\)
Thể tích nước hiện có trong bể cá :
\(50\cdot\frac{1}{4}=12,5(dm^3)\)
95% thể tích nước có trong bể là :
\(\frac{50\cdot95}{100}=47,5(dm^3)\)
Số lít nước cần đổ thêm vào bể là :
47,5 – 12,5 = 35 (dm3) = 35l
Đáp số : 35l
BÀI GIẢI
Đổi: 25cm = 2,5dm
40cm = 4dm
50cm = 5dm
Thể tích của bể cá là :
2,5 x4 x5= 50 (dm3)
Thể tích nước hiện có trong bể cá :
50·14 = 12,5(dm3)
95% thể tích nước có trong bể là :
50 :100 x 95= 47,5(dm3)
Số lít nước cần đổ thêm vào bể là :
47,5 – 12,5 = 35 (dm3) = 35l
Đáp số : 35l

Diện tích hình thang ABED:
( 2,5 + 1,6 ) x 1,2 :2 = 2,46 ( dm2)
Chiều cao của hình BEC cũng là chiều cao của hình thang ABED.
Diện tích hình tam giác BEC:
1,3 x 1,2 : 2 = 0,78 ( dm2)
Diện tích hình thang ABED lớn hơn diện tích của hình tam giác BEC:
2,46 - 0,78 = 1,68 ( dm2)
Đáp số : 1,68 dm2
Bài này bạn cần nhìn kĩ hơn một chút.
Đôi khi, có những bài toán bạn nên để ý những điểm ngoài cùng của hình.\
Mình chỉ nhắn nhủ vậy thôi!

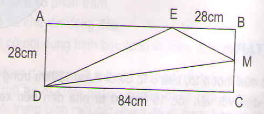
Diện tích hình chữ nhật ABCD là:
28 x 84=2352(cm2)
độ dài cạnh BM hay MC là:
28:2=14(cm)
Độ dài cạnh AE là:
84-28=56(cm)
Diện tích hình tam giác AED là:
28 x 56:2=784(cm2)
Diện tích hình tam giác EBM là:
28 x 14:2=196(cm2)
Diện tích hình tam giác MDC là:
84 x 14 : 2=588(cm2)
Diện tích tam giác EDM là:
2352-784-196-588=784(cm2)
Đáp số:784cm2
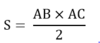

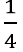 thể tích của bể có chứa nước. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để 95% thể tích của bể có chứa nước ?
thể tích của bể có chứa nước. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để 95% thể tích của bể có chứa nước ?

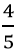 chiều cao của bể. Hỏi chiều cao của bể bằng bao nhiêu xăng-ti-mét ?
chiều cao của bể. Hỏi chiều cao của bể bằng bao nhiêu xăng-ti-mét ?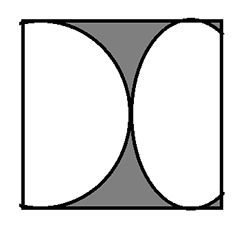

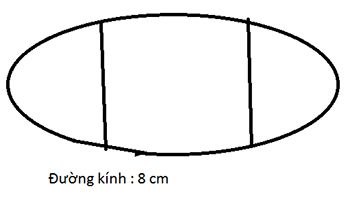



Diện tích hình tam giác DEG là:
5 × 4 : 2 = 10 ( c m 2 )