Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
S 1 = ∫ 0 k e x sin x d x ; S 2 = ∫ k π e x sin x d x S = S 1 + S 2 = ∫ 0 π e x sin x d x
2 S 1 + 2 S 2 - 1 = 2 S 1 - 1 2
⇔ S 2 = 2 S 1 2 - 2 S 1 + 1 - S = 0 ⇔ 2 ∫ 0 k e x sin x d x 2 - 2 ∫ 0 k e x sin x d x + 1 - ∫ 0 k e x sin x d x = 0
Tính toán trực tiếp qua các đáp án ta thấy PT trên đúng với k = π 2
Đáp án cần chọn là B

Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2

Đáp án C
Thể tích khối tròn xoay cần tính là V H = π . ∫ 1 k lnx d x ⇒ I = ∫ 1 k lnx d x .
Đặt u = ln x d v = d x ⇔ d u = d x x v = x suy ra I = x . ln x 1 k - ∫ 1 k d x = x . ln x - 1 1 k = k . ln k - 1 + 1 .
Mặt khác V H = π . I = π ⇒ I = 1 suy ra k . ln k - 1 + 1 = 1 ⇔ k . ln k - 1 = 0 ⇔ k = e .

Đáp án A
S = ∫ 0 π cos x d x = ∫ 0 π / 2 cos x d x − ∫ π / 2 π cos x d x = sin x 0 π / 2 − sin x π / 2 π = 1 − 0 − 1 = 2.


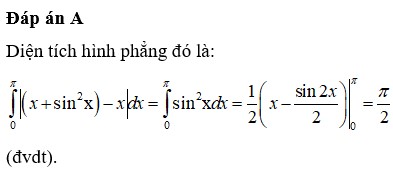
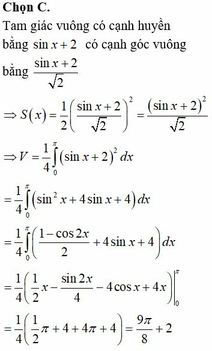
Ta có
x = sin πy ∈ - 1 ; 1 ⇒ x + 1 ≥ 0
Mà 0 ≤ y ≤ 1 nên y = x + 1 2 ⇔ x = y - 1
Vậy S = ∫ 0 1 sin πy - y + 1 d y = 2 π + 1 3
Đáp án B