Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)
vì ABCD là hình bình hành
=> AD // BC ( tính chất )
=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)
=> \(\widehat{B}=180^0-110^0=70^0\)
Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH
Xét tam giác vuông ABH, có:
AH=AB*sin B=12*sin 70 độ
\(AH\approx11,276\)(cm)
ta có: AD=BC ( ABCD là hình chữ nhật )
\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

110 12 15 M N R P Q
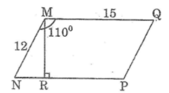
Giả sử hình bình hành \(MNPQ\) có \(MN=12cm,MQ=15cm,\widehat{MNQ}=110^o\)
Ta có \(\widehat{NMQ}+\widehat{MNP}=180^o\) ( hai góc trong cùng phía )
mà \(\widehat{NMQ}=110^o\)
\(\Rightarrow\widehat{MNP}=180^o-110^o=70^o\)
Kẻ \(MR\perp NP\)
Trong tam giác vuông \(MNR\) ta có :
\(MR=MN.sin\widehat{MNP}\)
\(=12.sin70^o\approx11,276\)
Vậy \(S_{MNPQ}=MR.MQ\approx11,276.15=169,14\left(cm^2\right)\)
Chúc bạn học tốt !!!

Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, ∠ NMQ = 1100
Ta có: ∠ NMQ + ∠ MNP = 180 ° (hai góc trong cùng phía)
Suy ra: ∠ MNP = 180 ° - ∠ NMQ
= 180 ° - 110 ° = 70 °
Kẻ MR ⊥ NP
Trong tam giác vuông MNR, ta có:
MR = MN.sin ∠ MNP =12.sin 70 ° ≈ 11,276 (cm)
Vậy S M N P Q = MN.NP ≈ 11,276.15 = 169,14 ( c m 2 )

Giả sử ta có hình bình hành ABCD, đường chéo AC, AB=12cm, AC=10cm, `\hat(ABC)=150^o`.
`S_(ABC) = 1/2 . 10. 12 . sinABC = 30 (cm^2)`
Vì đường chéo AC chia hình bình hành ABCD ra 2 tam giác bằng nhau.
`=> S_(ABCD) = 2.S_(ABC) = 60(cm^2)`
`=>` B.

Đặt \(\frac{AB}{BC}=\frac{3}{5}=x\Rightarrow AB=3x;BC=5x\)
Tam giác ABC vuông tại A, theo py ta go:
\(AB^2+AC^2=BC^2\Rightarrow9x^2+144=25x^2\Rightarrow16x^2=144\Leftrightarrow x^2=9\)
=> X = 3 ; AB = 3x = 3.3=9 ; BC= 5x = 5.3 = 15
TAm giac ABC vuông tại A theo hệ thức lượng
AH.BC = AB.AC => AH= (AB.AC)/BC = (9.12)/15 = 7,2cm
AB^2 = BC . BH => BH = AB^2 /BC = 9^2/15 = 5,4
=> HC = BC - HB = 15 - 5,4 = 9,6cm
VẬY AH = 7,2 ; BH = 5,4;CH = 9,6

A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)

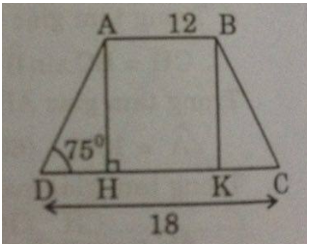
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=
Diện tích hình binh hành là 90\(\sqrt{3}\) (cm2)