Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M E F G H N P Q I K
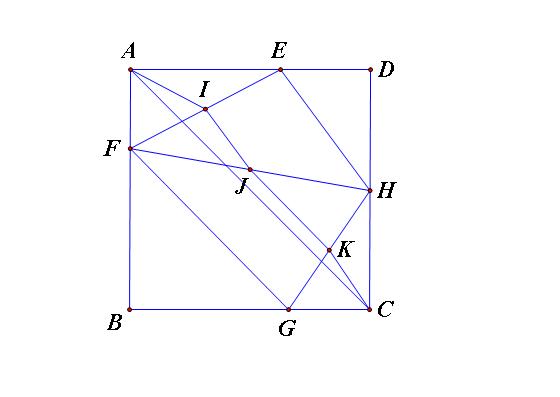
Gọi EFGH là tứ giác nội tiếp hình vuông
(\(E\in AB,F\in BC,G\in CD,H\in AD\)) , Từ E,F,G,H lần lượt dựng các đường thẳng vuông góc với BD tại P,Q,M,N; I và K là giao điểm của AG và EF.
Ta có : \(AI\ge AM=MP;GI\ge MP=GM;EK\ge EP=BP;KF\ge FQ=BK\)
\(\Rightarrow AG+EF=AI+IG+EK+KF\ge\left(PM+BQ\right)+\left(PN+BP\right)\)
Mặt khác, lại có : \(EH\ge NP;FG\ge MQ\)
\(\Rightarrow EF+FG+GH+HE\ge\left(PM+MQ+BQ\right)+\left(PN+NP+BP\right)\)
\(=BD+BD=2\)
\(\Rightarrow EF+FG+GH+GE\ge2\) (dpcm)
Ta có EF=2.AI,EH=2.IJ,GH=2.CK,EG=2.IK( Áp dụng tính chất đường trung bình và trung tuyến ứng với cạnh huyền trong tam giác vuông)
Suy ra \(P_{EFGH}=2\left(AI+IJ+JK+KC\right)\ge2AC=2\)

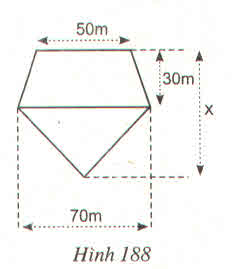
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

Bài giải:
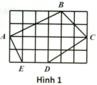
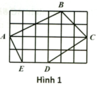
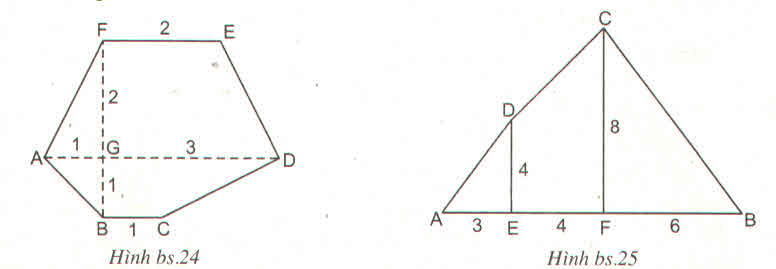
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

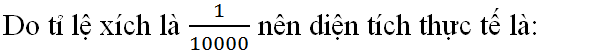
 AB.AE =
AB.AE =  hay 6x =
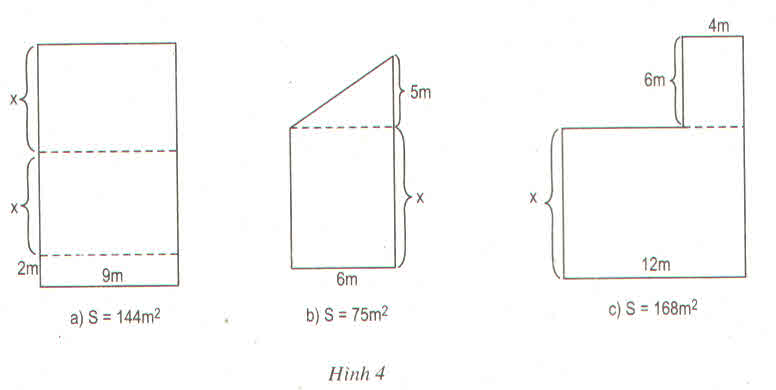
hay 6x = 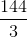



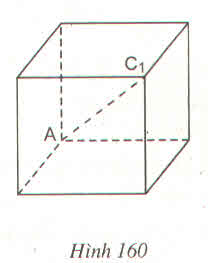
SABCDE
= SMNPQ - SABM - SBCN -SAQE - SDCP
= 24 - 12 = 12cm2