Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

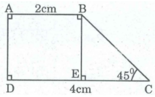
Giả sử hình thang vuông ABCD có:
∠ A = ∠ D = 90 0 ; ∠ C = 45 0
Kẻ BE ⊥ CD
Tam giác vuông BEC có ∠ (BEC) = 90 0 cân tại E ⇒ BE = EC
Hình thang ABCD có hai cạnh bên AD // BE (vì cùng vuông góc với DC) ⇒ DE = AB = 2cm
EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm ( vì tam giác BEC là tam giác vuông cân).
SABCD = 1/2 .BE(AB+ CD) = 1/2 .2.(2 + 4) = 6 ( c m 2 )

Xét hình thang vuông ABCD có: ˆA=ˆD=900;ˆC=450A^=D^=900;C^=450
Kẻ BE ⊥ CD
Trong tam giác vuông BEC có ˆBEC=900BEC^=900
ˆC=45∘⇒C^=45∘⇒∆ BEC vuông cân tại E
⇒ BE = EC
Hình thang ABED có hai cạnh bên AD // BE (vì cùng vuông góc với DC)
⇒ DE = AB = 2cm
EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm
SABCD=1/2.BE(AB+CD)=1/2.2.(2+4)=6(cm2)

C B A D 7cm 9cm 8cm 30 độ H
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}\).(7+9).4=32 cm2
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}.\left(7+9\right).4\)=32 cm2

Bài này có 2 cách nhưng mình chỉ giải 1 cách thôi,không biết có đúng không nhé!(Cho phép mình đặt tên các đỉnh)
Kẻ BE//AD =>Tam giác BEC là tam giác vuông.Vì góc BCE = 45 độ
=> Góc CBE= 45 độ =>Tam giác BEC vuông cân.=> BE=EC=DC-DE=9-6=3.
Diện tích của hình thang là:(a+b)*h:2=(AB+CD)*BE:2=(6+9)*3:2=45:2=22.5(cm vuông)

Kẻ \(BH\perp CD\)
Mà \(CD\perp AD\left(gt\right)\Rightarrow BH//AD\)
Hình thang ABHD (AB//HD) có BH//AD nên \(\hept{\begin{cases}HD=AB=5\left(cm\right)\\BH=AD\end{cases}}\) (t/c hình thang)
\(HD+HC=DC\Rightarrow5+HC=9\Rightarrow HC=4\left(cm\right)\)
\(\Delta HBC\)vuông cân tại H nên \(HB=HC=4cm\Rightarrow AD=4cm\left(AD=BH\right)\)
Áp dụng định lí Pitago tính được \(BC=\sqrt{32}\left(cm\right)\)
Chu vi hình thang vuông ABCD là:
\(AB+BC+CD+AD=5+\sqrt{32}+9+4=18+\sqrt{32}\left(cm\right)\)
Chúc bạn học tốt.

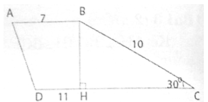
Giả sử hình thang ABCD (AB // CD) có AB = 7cm, BC = 10cm, CD = 11cm và
Kẻ BH ⊥ CD (H ∈ CD) Tam giác BHC vuông tại H lại có ∠C = 30o nên tam giác BHC là nửa tam giác đều. Suy ra
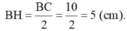
Diện tích hình thang ABCD là:
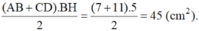
2 4 2 45 o A B C D E
Hạ đường cao CE thì EB = AB - AE = AB - DC = 4 - 2 =2.
Tam giác vuông EBC có góc B = 45 độ nên nó là tam giác vuông cân. Suy ra CE = EB = 2.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.CE=\dfrac{4+2}{2}.2=6\left(cm^2\right)\)