Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

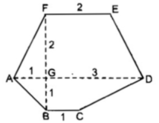
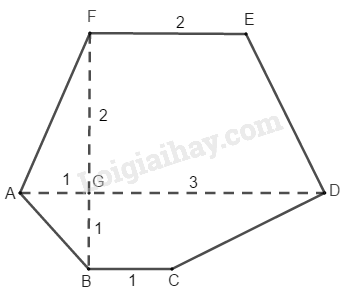
Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.
Hình thang ABCD có cạnh đáy BC = 1 (cm)
Đáy AD = AG + GD = 1 + 3 = 4 (cm)
Đường cao BG = 1 (cm)
S A B C D = (AD + BC) / 2.FG = (4 + 1) / 2 = 5/2 ( c m 2 )
Hình thang ADEF có đáy AD = 4 (cm)
S A D E F = (AD + EF) / 2.FG = (4 + 2) / 2. 2 = 6 ( c m 2 )
S A B C D E F = S A B C D + S A D E F = 5/2 + 6 = 17/2 ( c m 2 )
Đáy EF = 2cm, đường cao FG = 2cm

Ta có: AI⊥BD
CK⊥BD
Do đó: AI//CK
Xét tứ giác AKCI có
AK//CI
AI//CK
Do đó: AKCI là hình bình hành
=>AI=CK và AK=CI
Ta có: AK+KB=AB
CI+ID=CD
mà AK=CI và AB=AD
nên KB=ID
Xét ΔKFB vuông tại F và ΔIED vuông tại E có
KB=ID
\(\hat{KBF}=\hat{IDE}\) (hai góc so le trong, AB//CD)
Do đó: ΔKFB=ΔIED
=>BF=DE
1. Nhận xét đầu tiên
- Vì \(A E \bot B D\), \(C F \bot B D\) nên \(A E , C F\) cùng vuông góc với \(B D\).
👉 Suy ra \(A E \parallel C F\). - Mà trong hình bình hành: \(A B \parallel C D\).
👉 Vậy \(A E \parallel C F\) và chúng lại cắt \(A B , C D\). Điều này gợi ý tính chất đối xứng.
2. Xét tính chất để tìm ra hình đặc biệt
Trong hình bình hành, nếu từ hai đỉnh đối diện kẻ đường vuông góc tới đường chéo kia mà song song với nhau, thì hình bình hành này thường có tính đối xứng qua trung điểm đường chéo.
👉 Dễ đoán: \(A B C D\) là hình thoi.
Lý do: Trong hình thoi, hai đường chéo vuông góc và là trục đối xứng, nên việc kẻ vuông góc từ đỉnh xuống chéo sẽ tạo ra các đoạn đối xứng nhau.
3. Chứng minh chi tiết
- Vì \(A E \bot B D\), \(C F \bot B D\). Nên \(A E \parallel C F\).
- Mà \(A B \parallel C D\).
- Xét tứ giác \(A I C K\): có \(A I \parallel C K\) và \(I K \parallel A C\).
👉 Tứ giác \(A I K C\) là hình bình hành.
Trong hình bình hành này, \(A I = C K\). ✔ - Tương tự, vì đối xứng qua \(B D\), ta có \(D E = B F\). ✔
- Ngoài ra, do sự đối xứng này, \(A B = B C = C D = D A\).
👉 Vậy \(A B C D\) chính là hình thoi. ✔
✅ Kết quả cuối cùng:
- \(A B C D\) là hình thoi.
- \(A I = C K\).
- \(D E = B F\).
- tham khảo

Diện tích đa giác ABCDEF là:
\(S_{ABCDEF}=S_{FGA}+S_{FEDG}+S_{BCDG}+S_{AGB}\\ =\dfrac{2.1}{2}+\dfrac{\left(2+3\right).2}{2}+\dfrac{\left(1+3\right).1}{2}+\dfrac{1.1}{2}\\ =1+5+2+0,5\\ =8,5\left(cm^2\right)\)
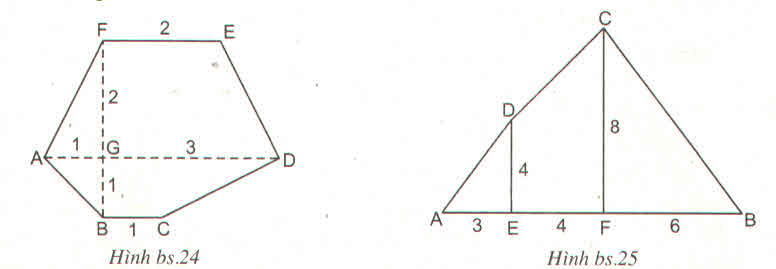

Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
S A E D = 1/2 AE.DE = 1/2. 3. 4 = 6( c m 2 )
S E D C F = (ED + FC)/2. EF = (4 + 8)/2. 4 = 24 ( c m 2 )
S C F B = 1/2 CF. FB = 1/2 .8 .6 = 24 ( c m 2 )
S A B C D = S A E D + S E D C F + S C F B = 6 + 24 + 24 = 54 ( c m 2 )