Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 0 ≤ sin 2 x ≤ 1 ⇒ 1 ≤ 4 - 3 sin 2 x ≤ 4
* y = 1 ⇔ sin 2 x = 1 ⇔ cos x = 0 ⇔ x = π 2 + k π
* y = 4 ⇔ sin 2 x = 0 ⇔ x = k π
Vậy giá trị lớn nhất của hàm số bằng 4, giá trị nhỏ nhất bằng 1.
Chọn B

a) \(y=\dfrac{4}{sin^22x-1}\)
Xác định khi và chỉ khi
\(sin^22x-1\ne0\)
\(\Leftrightarrow sin^22x\ne1\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x\ne1\\sin2x\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x\ne sin\dfrac{\pi}{2}\\sin2x\ne sin\dfrac{3\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x\ne\dfrac{\pi}{2}+k2\pi\\2x\ne\dfrac{3\pi}{2}+k2\pi\\2x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{3\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow x\ne\pm\dfrac{\pi}{4}+k\pi\)
Vậy tập xác định là \(D=R\)\\(\left\{\pm\dfrac{\pi}{4}+k\pi\right\}\)
2:
a: \(y=4+\left(cos^2x-sin^2x\right)+\left(cos^2x+sin^2x\right)\)
\(=4+1+cos2x=cos2x+5\)
-1<=cos2x<=1
=>-1+5<=cos2x+5<=1+5
=>4<=cos2x+5<=6
TGT là T=[4;6]
b: \(y=5-\dfrac{3}{2}\cdot2sinx\cdot cosx=-\dfrac{3}{2}sin2x+5\)
-1<=sin 2x<=1
=>-3/2<=-3/2sin2x<=3/2
=>-3/2+5<=y<=3/2+5
=>7/2<=y<=13/2
=>TGT là T=[7/2;13/2]
c: -1<=sin x<=1
=>-2<=-2sin x<=2
=>3<=-2sinx+5<=7
=>\(\dfrac{4}{3}>=\dfrac{4}{-2sinx+5}>=\dfrac{4}{7}\)
TGT là T=[4/7;4/3]

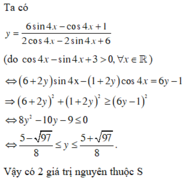


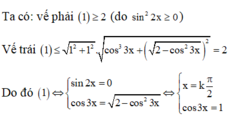
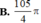
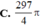
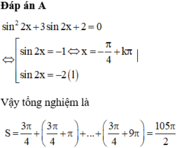

Chọn C.
Áp dụng , với u = 2 + sin22x.
y' = 3(2 + sin22x)2(2 + sin22x)’ = 3(2 + sin22x)2(sin22x)’.
Tính (sin22x)’, áp dụng với u = sin2x
(sin22x)’ = 2.sin2x(sin2x)’ = 2.sin2x.cos2x(2x)’ = 2sin4x.
⇒ y' = 6sin4x(2 + sin22x)2.