Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét hàm số y=\(\sqrt{x+\sqrt{x}}+\sqrt{x}\) . ta có
y'=\(\frac{\left(x+\sqrt{x}\right)}{2\sqrt{x+\sqrt{x}}}+\frac{1}{2\sqrt{x}}=\frac{1+\frac{1}{2\sqrt{x}}}{2\sqrt{x+\sqrt{x}}}+\frac{1}{2\sqrt{x}}\)
=\(\frac{1+2\sqrt{x}}{4\sqrt{x}\sqrt{x+\sqrt{x}}}+\frac{1}{2\sqrt{x}}=\frac{1+2\sqrt{x}+2\sqrt{x+\sqrt{x}}}{4\sqrt{x}\sqrt{x+\sqrt{x}}}\)

\(y'=\frac{e^x}{2\sqrt{e^x}}+3.e^{3x-1}-\left(-\sin x+\cos x\right)5^{\sin x+\cos x}\ln5\)
\(=\frac{\sqrt{e^x}}{2}+3e^{3x-1}+\left(\sin x+\cos x\right).5^{\sin x+\cos x}\ln5\)

xét hàm số y=ln(\(x+\sqrt{1+x^2}\))
Ta có
y'=\(\frac{1}{x+\sqrt{1+x^2}}\left(1+\frac{x}{\sqrt{1+x^2}}\right)=\frac{1}{x+\sqrt{1+x^2}}.\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\frac{1}{\sqrt{1+x^2}}\)

1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

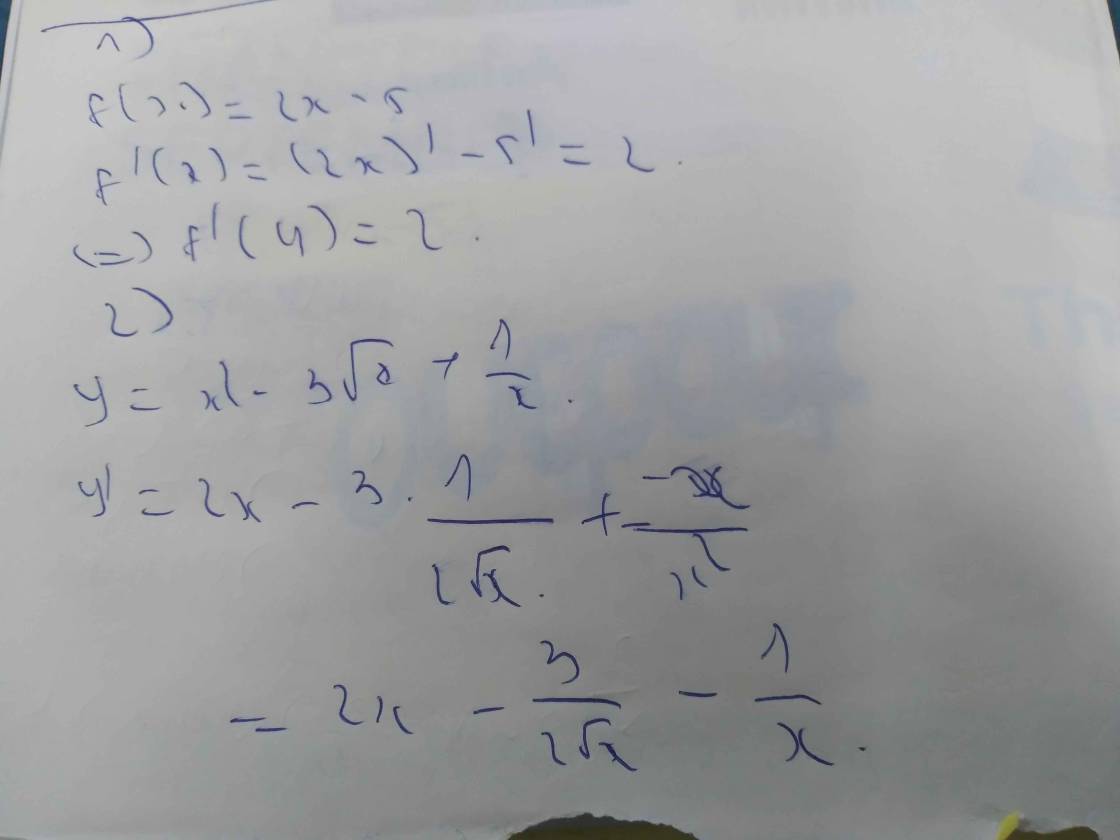

\(f'\left(x\right)=\dfrac{\left(4-3x\right)'}{2\sqrt{4-3x}}=\dfrac{-3}{2\sqrt{4-3x}}\)
\(\Rightarrow f'\left(-4\right)=\dfrac{-3}{2\sqrt{4-3.\left(-4\right)}}=-\dfrac{3}{8}\)