Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S = 1/3 + 1/3^2 + 1/3^3 + 1/3^4 + ... + 1/3^99 + 1/3^100
3S = 1 +1/3 +1/3^2 +1/3^3 + ... + 1/3^98 +1/3^99
3S - S = ( 1 + 1/3 + 1/3^2 +1/^3 + ... + 1/3^98 +1/3^99 ) - ( 1/3 + 1/3^2 + 1/3^3 + 1/3^4 +... + 1/3^99 + 1/3^100 )
2S = 1 - 1/3^100
S = (1 - 1/3^100). 1/2

`3A=-1+1/3-1/3^2+.....+1/3^99-1/3^100`
`=>3A+A=4A=-1-1/3^101`
`=>A=(-1-1/3^101)/4`

Ta có :
\(D=\dfrac{100-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+.......+\dfrac{99}{100}}\)
\(\Leftrightarrow D=\dfrac{100-1-\dfrac{1}{2}-\dfrac{1}{3}-......-\dfrac{1}{100}}{\dfrac{1}{2}+\dfrac{2}{3}+.....+\dfrac{99}{100}}\)
\(\Leftrightarrow D=\dfrac{99-\dfrac{1}{2}-\dfrac{1}{3}-......-\dfrac{1}{100}}{\dfrac{1}{2}+\dfrac{2}{3}+....+\dfrac{99}{100}}\)
\(\Leftrightarrow D=\dfrac{\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+.....+\left(1-\dfrac{1}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+.......+\dfrac{99}{100}}\)
\(\Leftrightarrow D=\dfrac{\dfrac{1}{2}+\dfrac{2}{3}+........+\dfrac{99}{100}}{\dfrac{1}{2}+\dfrac{2}{3}+......+\dfrac{99}{100}}=1\)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\\ \Leftrightarrow3A=3\left(+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\ =1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
Lấy 3A - A ta được
\(3A-A=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\
2A=1-\dfrac{1}{3^{100}}\\
\Leftrightarrow A=\dfrac{1-\dfrac{1}{3^{100}}}{2}\)

D = \(\dfrac{1}{2}+\dfrac{ 1}{2^2}+\dfrac{1}{2^3}+....+\dfrac{1}{2^{100}}\)
D = \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}+\dfrac{1}{2^{100}}\)
2x D = \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}\)
2D - D = 1 - \(\dfrac{1}{2^{100}}\)
D = 1 - \(\dfrac{1}{2^{100}}\)
\(D=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+....+\dfrac{1}{2^{100}}\\ =>2D=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}\\ =>2D-D=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right)\\ =>D=1-\dfrac{1}{2^{100}}=\dfrac{2^{100}-1}{2^{100}}\)

2)
\(D=\dfrac{4}{3}+\dfrac{10}{9}+\dfrac{28}{27}+...+\dfrac{3^{98}+1}{3^{98}}\\ D=\dfrac{3+1}{3}+\dfrac{3^2+1}{3^2}+\dfrac{3^3+1}{3^3}+...+\dfrac{3^{98}+1}{3^{98}}\\ D=\dfrac{3}{3}+\dfrac{1}{3}+\dfrac{3^2}{3^2}+\dfrac{1}{3^2}+\dfrac{3^3}{3^3}+\dfrac{1}{3^3}+...+\dfrac{3^{98}}{3^{98}}+\dfrac{1}{3^{98}}\\ D=1+\dfrac{1}{3}+1+\dfrac{1}{3^2}+1+\dfrac{1}{3^3}+...+1+\dfrac{1}{3^{98}}\\ D=\left(1+1+1+...+1\right)+\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}\right)\\ D=98+\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}\right)\)
Gọi \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}\) là \(C\)
\(C=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}\\ 3C=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}\\ 3C-C=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{97}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}\right)\\ 2C=1-\dfrac{1}{3^{98}}\\ C=\left(1-\dfrac{1}{3^{98}}\right):2\\ C=1:2-\dfrac{1}{3^{98}}:2\\ C=\dfrac{1}{2}-\dfrac{1}{3^{98}\cdot2}\)
\(D=98+C=98+\dfrac{1}{2}-\dfrac{1}{3^{98}\cdot2}=98\dfrac{1}{2}-\dfrac{1}{3^{98}\cdot2}< 100\)
Vậy \(D< 100\)

D=\(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\)
=>3D=1+\(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
=>3D-D=(1+\(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\))-(\(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\))
=>2D=1-\(\dfrac{1}{3^{100}}< 1\)
=>D<\(\dfrac{1}{2}\)
Vậy...
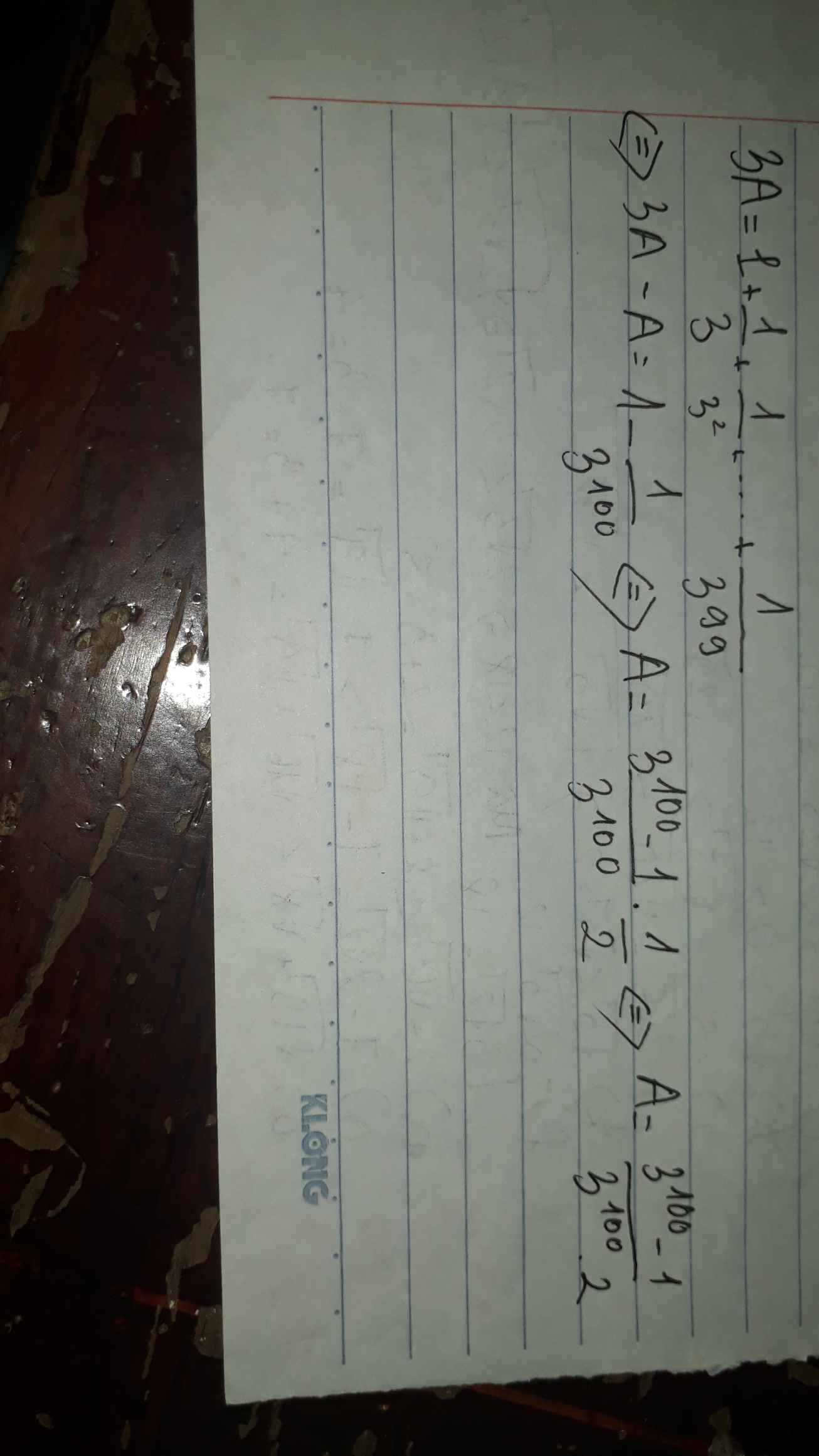
D=13+132+133+...+13100D=13+132+133+...+13100
⇔3D=1+13+132+...+399⇔3D=1+13+132+...+399
⇔3D−D=(1+13+132+...+1399)−(13+132+133+...+13100)⇔3D-D=(1+13+132+...+1399)-(13+132+133+...+13100)
⇔2D=1+1
SAI RỒI