
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với 0 ° < α < 90 ° ta có α tăng thì cos α giảm
Ta có: 40 ° < 75 ° , suy ra cos 40 ° > cos 75 °

Với 0 ° < α < 90 ° ta có α tăng thì sin α tăng
Ta có: 38 ° + 52 ° = 90 ° , suy ra: cos 38 ° = sin 52 °
Vì 38 ° < 52 ° nên sin 38 ° < sin 52 ° hay sin 38 ° < cos 38 °

Với 0 ° < α < 90 ° ta có α tăng thì cos α giảm
Ta có: 40 ° + 50 ° = 90 ° , suy ra: sin 50 ° = cos 40 °
Vì 40 ° < 50 ° nên cos 40 ° > cos 50 ° hay sin 50 ° > cos 50 °

a) Dùng bảng: sin 70 ° 13 ' ≈ 0 , 9410
- Cách nhấn máy tính:

b) cos 25 ° 32 ' ≈ 0 , 9023
- Cách nhấn máy tính:

c) t g 43 ° 10 ' ≈ 0 , 9380
- Cách nhấn máy tính:

d) c o t g 32 ° 15 ' ≈ 1 , 5850
- Cách nhấn máy tính:


sin 39 ° 13 ' ≈ 0,6323 cos 52 ° 18 ' ≈ 0,6115
tg 13 ° 20 ' ≈ 0,2370 cotg 10 ° 17 ' ≈ 0,5118
sin 45 ° ≈ 0,7071 cos 45 ° ≈ 0,7071
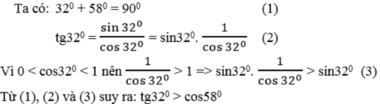
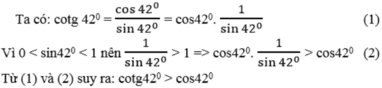


A B C D E
Để dễ hình dung, ta vẽ tam giác ABC vuông tại A, có DE là đường trung trực của cạnh BC ( D thuộc BC, E thuộc AC)
Giả sử góc C = 15 độ , độ dài đoạn AB = 1 (đvđd)
Ta có : Tam giác EBC cân tại E => Góc CBE = Góc C = 15 độ.
Ta có : Góc ABC = 75 độ => Góc ABE = 75 độ - 15 độ = 60 độ.
Suy ra EB = \(\frac{1}{Cos60}=2\) (đvđ.d) ; EA = \(Sin60.EB=\frac{\sqrt{3}}{2}.2=\sqrt{3}\)(đvđ.d) => AC = \(2+\sqrt{3}\)(đvđ.d)
Vì D là trung điểm BC nên ta có CD = DB = \(\frac{BC}{2}=\frac{\sqrt{AB^2+AC^2}}{2}=\frac{\sqrt{1^2+\left(2+\sqrt{3}\right)^2}}{2}=\sqrt{\frac{8+4\sqrt{3}}{4}}=\sqrt{2+\sqrt{3}}\) (đvđ.d)
\(Cos15=\frac{CD}{CE}=\frac{\sqrt{2+\sqrt{3}}}{2}=\frac{\sqrt{2}.\sqrt{4+2\sqrt{3}}}{4}=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}=\frac{\sqrt{6}+\sqrt{2}}{4}\)