Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)\(A=\frac{b\left(2a\left(a+5b\right)+\left(a+5b\right)\right)}{a-3b}.\frac{a\left(a-3b\right)}{ab\left(a+5b\right)}=\frac{b\left(a+5b\right)\left(2a+1\right).a\left(a-3b\right)}{\left(a-3b\right).ab\left(a+5b\right)}\)
\(A=2a+1\)=>lẻ với mọi a thuộc z=> dpcm
2) từ: x+y+z=1=> xy+z=xy+1-x-y=x(y-1)-(y-1)=(y-1)(x-1)
tường tự: ta có tử của Q=(x-1)^2.(y-1)^2.(z-1)^2=[(x-1)(y-1)(z-1)]^2=[-(z+y).-(x+y).-(x+y)]^2=Mẫu=> Q=1
3) kiểm tra lại xem đề đã chuẩn chưa

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
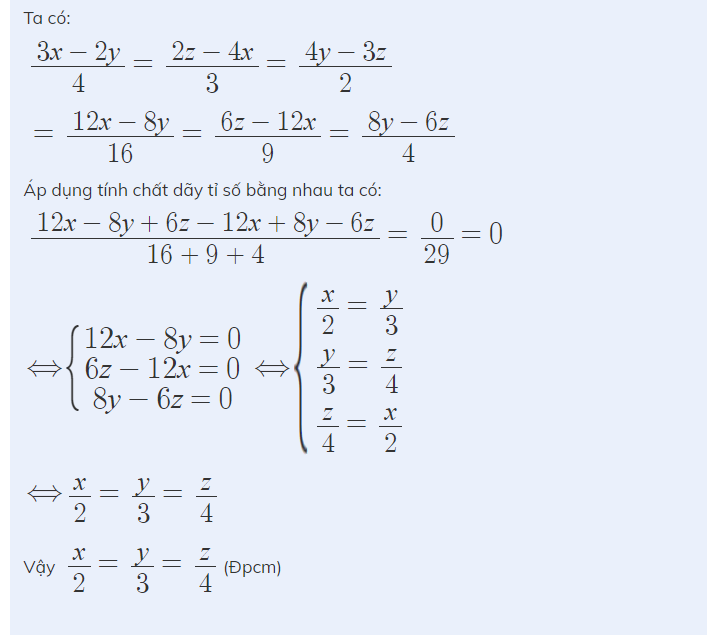

\(x^3+y^3+z^3=3xyz\)
\(x^3+y^3+z^3-3xyz=0\)
\(\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)=0\)
\(x^2+y^2+z^2-xy-xz-yz=0\left(x+y+z\ne0\right)\)
\(2\times\left(x^2+y^2+z^2-xy-xz-yz\right)=0\times2\)
\(2x^2+2y^2+2z^2-2xy-2xz-2yz=0\)
\(x^2-2xy+y^2+x^2-2xz+z^2+y^2-2yz+z^2=0\)
\(\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2=0\)
\(\left[\begin{array}{nghiempt}x-y=0\\x-z=0\\y-z=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=y\\x=z\\y=z\end{array}\right.\)
x = y = z
\(P=\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{x}{z}\right)\)
\(=\left(1+\frac{x}{x}\right)\left(1+\frac{y}{y}\right)\left(1+\frac{z}{z}\right)\)
\(=\left(1+1\right)\left(1+1\right)\left(1+1\right)\)
\(=2^3\)
\(=8\)

Áp dụng bđt côsi cho 2 số dương lần lượt ta có :
\(1+\frac{y}{x}\ge2\sqrt{\frac{y}{x}}\)
\(1+\frac{z}{y}\ge2\sqrt{\frac{z}{y}}\)
\(1+\frac{x}{z}\ge2\sqrt{\frac{x}{z}}\)
Nhân vế theo vế ta đc : \(\left(1+\frac{y}{x}\right)\left(1+\frac{z}{y}\right)\left(1+\frac{x}{z}\right)\ge8\sqrt{\frac{xyz}{xyz}}=8\)
Dấu = xảy ra khi : \(1=\frac{y}{x}\)=> x=y và \(1=\frac{z}{y}\) => z=y và \(1=\frac{x}{z}\) => x=z
=> x=y=z
Thay vào M ta được : \(M=\frac{x^2}{2x^2}+\frac{y^2}{2y^2}+\frac{z^2}{2z^2}=\frac{3}{2}\).

\(\frac{x-y-z}{x}=\frac{y-x-z}{y}=\frac{z-x-y}{z}=\frac{x-y-z+y-x-z+z-x-y}{x+y+z}=\frac{-x-y-z}{x+y+z}=-1\)
\(\rightarrow\begin{cases}x-y-z=-x\\y-x-z=-y\\z-x-y=-z\end{cases}\)
\(\leftrightarrow\begin{cases}y+z=2x\\z+x=2y\\x+y=2z\end{cases}\)
\(A=\frac{x+y}{z}.\frac{y+z}{x}.\frac{z+x}{y}=8\)

\(\frac{\left(z-x\right)+\left(x-y\right)+\left(y-z\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=0\)
Trả lời:
Ta có x-y-z=0
-> x=y+z (1)
C= (1-\(\frac{x}{z}\))(1-\(\frac{x}{y}\))(1+\(\frac{y}{z}\))
C=\(\frac{\left(x-z\right)\left(y-x\right)\left(z+y\right)}{xyz}\)
C= \(\frac{\left(y+z-z\right)\left(y-\left(y+z\right)\right)\left(z+y\right)}{yz\left(y+z\right)}\)
C= \(\frac{y.-z.\left(z+y\right)}{y.z.\left(y+z\right)}\)
C=-1
Đáp số: C=-1
Hình như đề sai hay sao ý?