Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều chiều rộng là x ( x > 0)
Chiều dài là: 3( x - 2) - 3 = 3x - 9
Diện tích hình chữ nhật lúc đầu là: x(3x-9) = 3x2 - 9x
Diện tích hình chữ nhật sau khi tăng mỗi cạnh thêm 3cm là:
(x+3)(3x-9+3) = (x+3)(3x -6) = 3x2 + 9x - 6x - 18 = 3x2 + 3x - 18
Theo bài ra ta có: 3x2 + 3x - 18 - (3x2 -9x) = 66
12x - 18 = 66
12x = 66 + 18
12x = 84
x = 7
Chiều rộng là 7
chiều dài là: 7 x 3 - 9 = 12
Chu vi ( 12 + 7) x 2 = 38 (cm)
Kết luận : Chu vi hình chữ nhật 38 cm
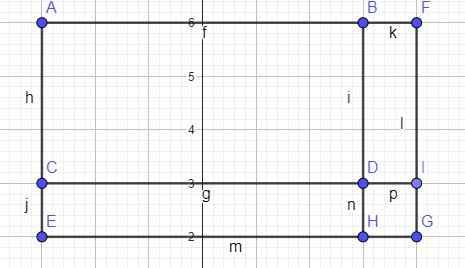
Diên tích DIGH là :
3.3 = 9 (cm²)
Tổng diện tích CDHE và FBDI là :
3.(BD+CD)=66-9=57 cm²
BD+CD = 57:3 = 19 cm
Vậy chu vi hình chữ nhật là
19.2 = 38 cm
#Toán lớp 9

Gọi chiều dài, chiều rộng của hình chữ nhật lần lượt là a(cm),b(cm)
(Điều kiện: a>0 và b>0)
Chiều dài của hình chữ nhật sau khi giảm đi 2cm là a-2(cm)
Chiều rộng của hình chữ nhật sau khi tăng thêm 2 cm là b+2(cm)
Nếu giảm chiều dài đi 2cm và tăng chiều rộng thêm 2cm thì diện tích tăng thêm 4cm2 nên ta có:
(a-2)(b+2)=ab+4
=>ab+2a-2b-4=ab+4
=>2a-2b=8
=>a-b=4(1)
Chiều dài của hình chữ nhật sau khi giảm đi 3 lần là:
\(\dfrac{1}{3}a\left(cm\right)\)
Chiều rộng của hình chữ nhật sau khi tăng thêm 2 lần là:
2b(cm)
Khi giảm chiều dài đi 3 lần và tăng chiều rộng thêm 2 lần thì chu vi không đổi nên ta có:
\(\dfrac{1}{3}a+2b=a+b\)
=>\(\dfrac{1}{3}a-a=b-2b\)
=>\(-\dfrac{2}{3}a=-b\)
=>\(b=\dfrac{2}{3}a\)(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=4\\\dfrac{2}{3}a=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b=4\\\dfrac{2}{3}a-b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{3}a=4\\a-b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=12\\b=a-4=12-4=8\end{matrix}\right.\left(nhận\right)\)
Diện tích hình chữ nhật là:
\(12\cdot8=96\left(cm^2\right)\)
Gọi chiều dài ban đầu của hình chữ nhật là L và chiều rộng ban đầu là W.
Theo đề bài, ta có hệ phương trình sau:
(L - 2)(W + 2) = LW + 4 (1) (diện tích tăng 4cm² khi giảm chiều dài đi 2cm và tăng chiều rộng thêm 2cm)
3L(W x 2) = 2(L + W) (2) (chu vi không đổi khi giảm chiều dài đi ba lần và tăng chiều rộng hai lần)
Giải hệ phương trình (1) và (2):
Mở ngoặc trong phương trình (1):
LW - 2L + 2W - 4 = LW + 4
-2L + 2W - 4 = 4
-2L + 2W = 8 (3)
Phương trình (2) có thể viết lại thành:
6LW = 2L + 2W (4)
Từ phương trình (3), ta có:
-2L = 8 - 2W
L = -4 + W (5)
Thay (5) vào (4):
6(-4 + W)W = 2(-4 + W) + 2W
-24W + 6W^2 = -8 + 2W + 2W
6W^2 - 24W = -8 + 4W
6W^2 - 28W + 8 = 0
Chia cả hai vế cho 2:
3W^2 - 14W + 4 = 0
Giải phương trình trên, ta được hai giá trị của W:
W1 ≈ 0.47 và W2 ≈ 4.53
Thay W1 và W2 vào phương trình (5), ta tính được hai giá trị của L:
L1 ≈ -3.53 và L2 ≈ 4.53
Vì chiều dài và chiều rộng không thể là giá trị âm, nên ta chỉ xét giá trị dương.
Vậy, chiều dài và chiều rộng của hình chữ nhật là L2 ≈ 4.53 và W2 ≈ 4.53.
Diện tích của hình chữ nhật là S = L2 * W2 ≈ 4.53 * 4.53 ≈ 20.52 cm².

Câu hỏi của Fun Mega - Toán lớp 9 - Học toán với OnlineMath

Gọi chiều dài và chiều rộng lần lượt là a,b
Theo đề, ta có: (a+1)(b+1)=ab+13 và (a-2)(b-1)=ab-15
=>ab+a+b+1=ab+13 và ab-a-2b+2=ab-15
=>a+b=12 và -a-2b=-17
=>a=7 và b=5

gọi chiều dài hcn là x, chiều rộng hcn là y (x>10,y>0)
=>diên tích hcn là xy
theo bài ra ta có
2y.(10-x)=xy+200
hình như thiếu dữ kiên
tiếp :
chu vi hcn bằng 100 nên ta có pt
\(\left(x+y\right)2=100\)
từ 2 pt ta có hệ\(\hept{\begin{cases}20y-2xy=xy+200\\2x+2y=100\end{cases}}\) <=>\(\hept{\begin{cases}20y-3xy-200=0\\x+y=50\end{cases}}\) <=>\(\hept{\begin{cases}20y-3\left(50-y\right)y=200\\x=50-y\end{cases}}\) <=> bạn tự giải...

đề hình như sai bạn à, tại sao lại là kích thước của 1 km?? @@