Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AM = x (m) ⇒ MC = BC – AM = 80 – x (m)
Xét tam giác BAM vuông tại A: AB = AM \(tan\widehat{AMB}=x.tan60^o=x.\sqrt{3}\left(m\right)\)
Xét tam giác DCM vuông tại C: \(CD=MC.tan\widehat{CMB}=\left(80-x\right).tan30^o=\frac{\sqrt{3}}{3}.\left(80-x\right)\left(m\right)\)
Vì hai trụ điện cùng chiều cao ⇒AB = CD
\(\Rightarrow x.\sqrt{3}=\frac{\sqrt{3}}{3}\left(80-x\right)\Leftrightarrow3x=80-x\Leftrightarrow4x=80\Rightarrow x=20\left(m\right)\)
\(\Rightarrow AM=20m;MC=80-20=60\left(m\right);AB=CD=20\sqrt{3}\approx34,64m\)
Chúc bạn học tốt !!!

Phần diện tích xung quanh còn lại (không kể phần lõm)
S 1 = 2. π .3.4. (11/12) =22π ( c m 2 )
Diện tích còn lại của hai đáy :
S 2 = 2. π . 3 2 . (11/12) =33 π 2 ( c m 2 )
Diện tích phần lõm là diện tích của hai chữ nhật kích thước 3cm và 4cm
S 3 = 2.3.4=24 ( c m 2 )
Diện tích toàn bộ hình sau khi đã cắt:
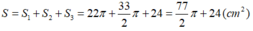

Thể tích hình trụ : V= π . r 2 .h = π . 3 2 .4 = 36π( c m 3 )


Diện tích xung quanh hình trụ bằng 314 c m 2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2 π r 2 = 31 ⇒ r 2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π ⋅ r 2 h = π ⋅ r 3 ≈ 1109 , 65 cm 3
Kiến thức áp dụng
Hình trụ có bán kính đáy r, chiều cao h thì:
+ Diện tích xung quanh: Sxq = 2πrh
+ Thể tích: V = π.r2.h

Diện tích xung quanh hình trụ bằng 314cm2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2πr2 = 314
⇒ r2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π.r2.h = π.r3 ≈ 1109,65 (cm3).

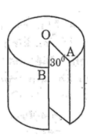
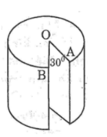
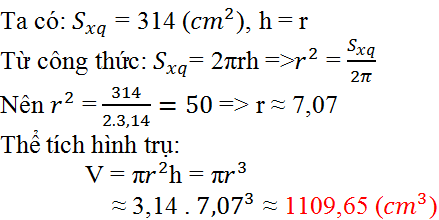
Gọi chiều cao của trụ điện thứ nhất là AB, chiều cao của trụ điện thứ hai là DC, với A và C lần lượt là chân của hai trụ điện
Ta sẽ có hình vẽ sau:
Theo đề, ta có: AC=80(m) và AB=CD
Xét ΔABM vuông tại A có \(\tan AMB=\frac{AB}{AM}\)
=>\(AM=\frac{AB}{\tan60}=\frac{AB}{\sqrt3}\)
Xét ΔDCM vuông tại C có \(\tan DMC=\frac{DC}{CM}\)
=>\(MC=\frac{DC}{\tan30}=\frac{AB}{\tan30}=AB\cdot\sqrt3\)
Ta có AM+MC=AC
=>\(\frac{AB}{\sqrt3}+AB\sqrt3=80\)
=>\(AB\left(\sqrt3+\frac{1}{\sqrt3}\right)=80\)
=>\(AB\cdot\frac{4}{\sqrt3}=80\)
=>\(AB=80:\frac{4}{\sqrt3}=\frac{80\sqrt3}{4}=20\sqrt3\left(m\right)\)
=>AB≃34,64(m)
=>Chiều cao của mỗi trụ điện là khoảng 34,64(m)
Ta có: \(MA=\frac{AB}{\sqrt3}=\frac{20\sqrt3}{\sqrt3}=20\left(m\right)\)
=>Khoảng cách từ M đến gốc của trụ điện thứ nhất là 20(m)
ta có: \(MC=AB\cdot\sqrt3=20\sqrt3\cdot\sqrt3=60\left(m\right)\)
=>Khoảng cách từ M đến gốc của trụ điện thứ hai là 60(m)