
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\Leftrightarrow2x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(b,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3+x>0\\2x-5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\2x-5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{5}{2}\\x< -3\end{matrix}\right.\)
\(c,\Leftrightarrow x\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-3< x< 0\)
\(d,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0\\x+5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\x+5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-3\\x< -5\end{matrix}\right.\)
\(e,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-2x\ge0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-2x\le0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x\le\dfrac{3}{2}\)

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
b: Ta có: ΔABE=ΔACD
nên BE=CD
c: Xét ΔDBC và ΔECB có
DB=EC
DC=EB
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KCB}=\widehat{KBC}\)
hay ΔKBC cân tại K
d: Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
Do đó: ΔABK=ΔACK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC

Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC

Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)

có \(\angle\left(BOC\right)+\angle\left(COA\right)=180^o\)(kề bù)\(=>\angle\left(COA\right)=180^0-\angle\left(BOC\right)=180-60=120^o\)
\(=>\angle\left(COA\right)=\angle\left(BOD\right)=120^o\)(đối đỉnh)
\(\angle\left(AOD\right)=\angle\left(BOC\right)=60^o\)(đối đỉnh)
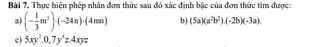



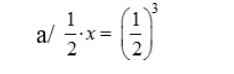 giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
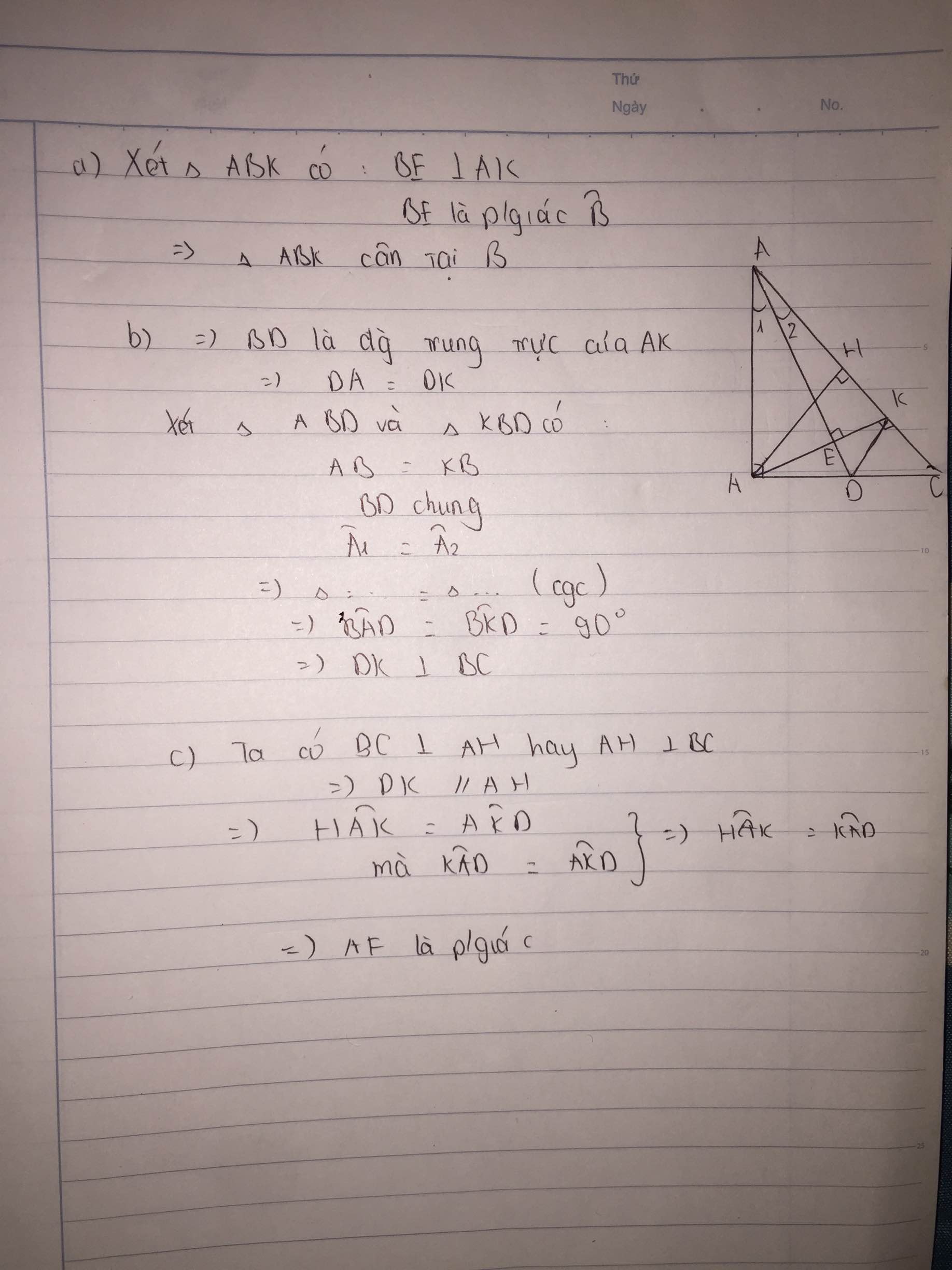


dốt toán : >>
:-|