K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
2
Q
1 tháng 12 2018
a) \(\widehat{A}=2\widehat{B}=6\widehat{C}\Leftrightarrow\frac{\widehat{A}}{2}=\frac{\widehat{B}}{6}=\frac{\widehat{C}}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có : \(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{6}=\frac{\widehat{C}}{1}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2+6+1}=\frac{180^o}{9}=20^o\)
\(\frac{\widehat{A}}{2}=20^o\Rightarrow\widehat{A}=20^o.2=40^o\)
\(\frac{\widehat{B}}{6}=20^o\Rightarrow\widehat{A}=20^o.6=120^o\)
\(\widehat{C}=20^o\)
Vậy ...
b,d tương tự
PT
1
PT
1
5 tháng 11 2021
a:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{\dfrac{1}{6}}=\dfrac{b}{\dfrac{1}{14}}=\dfrac{c}{\dfrac{1}{21}}=\dfrac{a+b+c}{\dfrac{1}{6}+\dfrac{1}{14}+\dfrac{1}{21}}=\dfrac{180}{\dfrac{2}{7}}=630\)
Do đó: a=105; b=45; c=30
NK
1
16 tháng 9 2017
Đặt \(\widehat{A}=2\widehat{B}=5\widehat{C}=k\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=k\\\widehat{B}=\frac{k}{2}\\\widehat{C}=\frac{k}{5}\end{cases}}\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=k+\frac{k}{2}+\frac{k}{5}=180^0\)
\(\Rightarrow\frac{17}{10}k=180^0\Leftrightarrow k=\frac{1800}{17}^0\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=\frac{1800}{17}^0\\\widehat{B}=\frac{900}{17}^0\\\widehat{C}=\frac{360}{17}^0\end{cases}}\)
NK
1
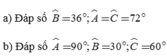
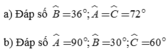
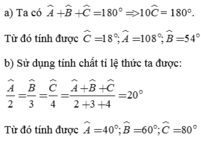
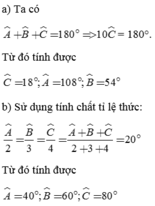
Ta có: \(\widehat{C}-\widehat{B}=36^0\Rightarrow\widehat{C}=\widehat{B}+36^0\)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow2\widehat{B}+\widehat{B}+\widehat{B}+36^0=180^0\Rightarrow\widehat{B}=36^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}=2\widehat{B}=72^0\\\widehat{C}=\widehat{B}+36^0=72^0\end{matrix}\right.\)