
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
2

Các câu hỏi dưới đây có thể giống với câu hỏi trên
NQ
1
HH
0

GD
2

PT
2

PT
1

11 tháng 10 2021
1125 : 1123- 35:9 - 60
1125: 1123- 243 : 9 - 60 121 - 243 : 9 - 60 = 34
PT
1

11 tháng 10 2021
125.100 - 25(9.4 +64)= 12500 - 25 (36+64) = 12500- 25.100=12500-2500=10000
PT
2

11 tháng 10 2021
\(=11^{25}\div11^{23}-3^5\div\left(1^{10}+2^3\right)-60\)
\(=11^{25}\div11^{23}-3^5\div\left(1+8\right)-60\)
\(=11^{25}\div11^{23}-3^5\div3^2-60\)
\(=11^2-3^3-60\)
\(=121-27-60\)
\(=34\)
NT
11 tháng 10 2021
f) 1125 : 1123 - 35 : (110 + 23) - 60
= 112 - 243 : (1 + 8 ) - 60
= 121 - 243 : ( 1+8 ) - 60
= 121 - 243 : 9 - 60
= 121- 27 - 60
= 94 - 60
= 34

TK
3
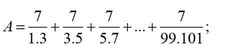
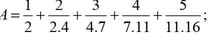
 mọi người làm bài 2 bài 3 giúp em với ạ (em cảm ơn)
mọi người làm bài 2 bài 3 giúp em với ạ (em cảm ơn)
 giúp mình với mọi người ơi mình xin đó
giúp mình với mọi người ơi mình xin đó

 Mình cảm ơn ạ
Mình cảm ơn ạ





1) A=\(\dfrac{7}{1.3}+\dfrac{7}{3.5}+\dfrac{7}{5.7}+...+\dfrac{7}{99.101}\)=\(\dfrac{7.2}{1.3.2}+\dfrac{7.2}{3.5.2}+\dfrac{7.2}{5.7.2}+...+\dfrac{7.2}{99.101.2}\)=
\(\dfrac{7}{2}\left(\text{}\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{101}\right)\)=\(\dfrac{7}{2}.\dfrac{100}{101}=\dfrac{350}{101}\)
2) A=\(\dfrac{1}{2}+\dfrac{2}{2.4}+\dfrac{3}{4.7}+\dfrac{4}{7.11}+\dfrac{5}{11.16}\)=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}\)
=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{16}\)=\(1-\dfrac{1}{16}=\dfrac{15}{16}\)