Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

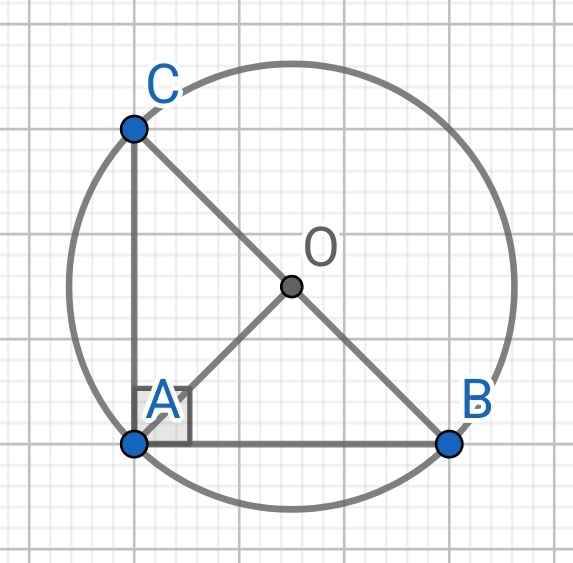
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= a² + a²
= 2a²
⇒ BC = a√2
Tâm của đường tròn ngoại tiếp ∆ABC là trung điểm của BC
Gọi O là trung điểm của BC khi đó bán kính là OA
⇒ OA = BC/2 = a√2/2

do tam giác vuông cân nội tiếp đường tròn => đường kính = độ dài cạnh huyền của tam giác vuông cân
bình phương cạnh huyền = tổng bình phương 2 cạnh góc vuông
=> bình phương cạnh huyền = 18
=> độ dài cạnh huyền = đường kính = \(3\sqrt{2}\)
=> bán kính = \(\frac{3\sqrt{2}}{2}\)

a: Bán kính là \(\dfrac{c}{2}\)
b: Bán kính là \(\dfrac{a\sqrt{2}}{2}\)

\(h=\sqrt{b^2-\frac{a^2}{4}}\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)
\(R=\frac{abb}{4S}=\frac{ab^2}{\sqrt{4b^2-a^2}.a}=\frac{b^2}{\sqrt{4b^2-a^2}}\)
\(r=\frac{S}{p}=\frac{a\sqrt{b^2-\frac{a^2}{4}}}{a+2b}\)

A B C I
trong tgiac vuông tâm đường tròn ngoại tiếp chính là trung điểm cạnh huyền
Áp dụng định lý pytago vào tgiac vuông ABC ta có :
\(BC^2\)=\(AC^2\)+\(AB^2\)
\(BC^2\)=\(8^2\)+\(6^2\)
\(BC^2\)=100
BC=10
Vậy bán kính đường tròn ngoại tiếp tgiac ABC là:
10:2=5cm

Gọi bk ngoại tiếp là R còn nôi tiếp là r ;p là 1/2 chu vi (= a+b+c/2)
ra có R=BC/2=5
mà S=pr=(6+8+10)/2r=6*8/2=>r=2